보의 처짐곡선/ 처짐각/ 휨응력도와 단면2차모멘트

앞에서 도심과 관련된 단면1차모멘트를 살펴보았습니다. 여기서는 보에서 발생하는 휨모멘트와 단면2차모멘트를 살펴보겠습니다.

 

▶이전글 단면정수 - 단면1차모멘트와 도심

 

보의 휨 변형

보나 슬래브에 생기는 응력을 이해하기 위해 보가 힘을 받을 때 변형되는 모양을 생각해봅시다. 만일 보와 기둥이 한 몸처럼 붙어 있다면 점선과 같이 아래로 휘어질 것입니다.

기둥과 강접합된 보의 변형

 

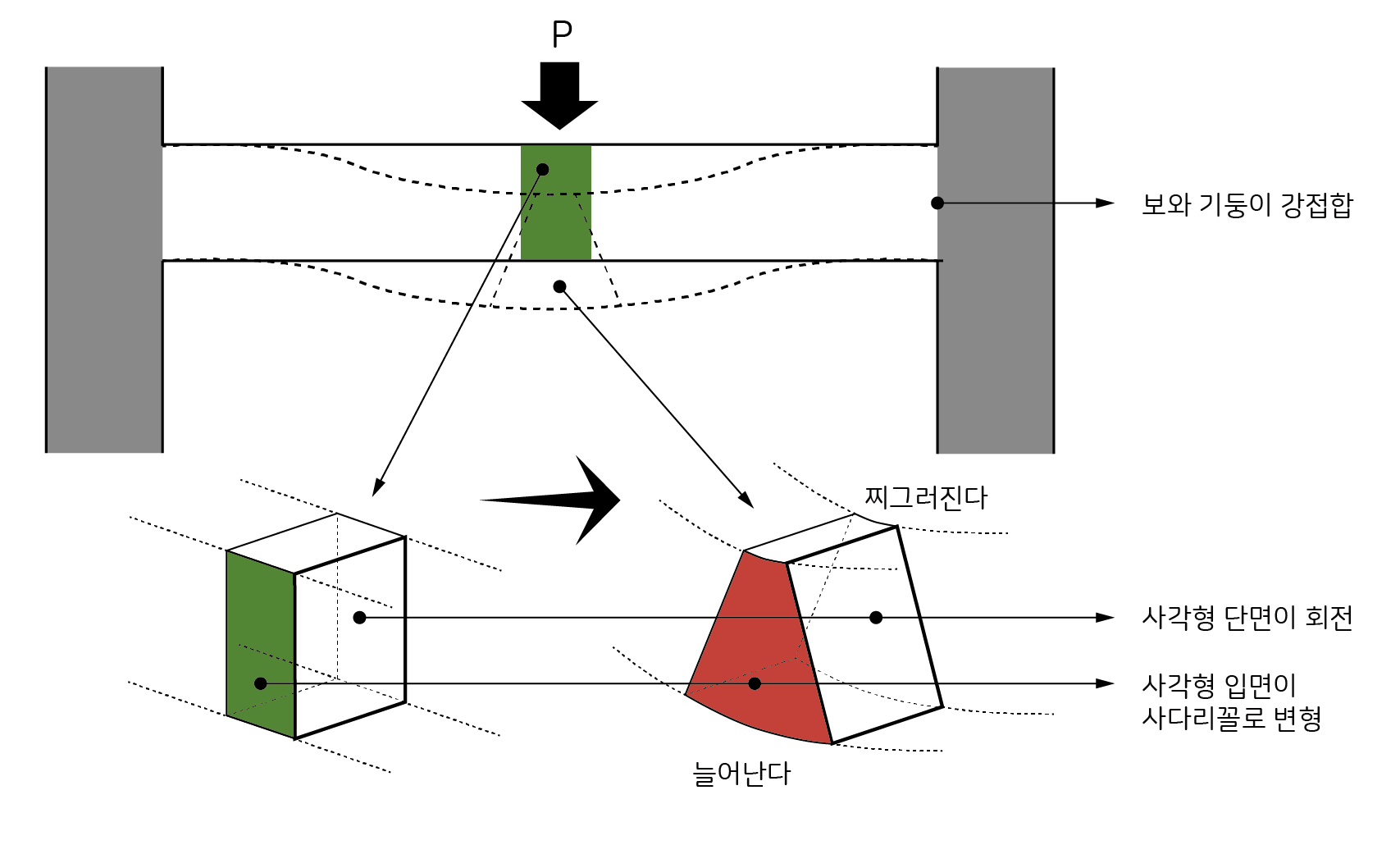
보의 한가운데에 있는 작은 육면체를 잘라서 어떻게 모양이 달라졌는지 살펴봅시다. 정면에서 보았을 때 힘을 받기 전에는 사각형이었던 입면(초록색)이 힘을 받은 후에는 사다리꼴(갈색)로 변형되었습니다. 변형되기 전에 사각형이었던 단면은 회전만 하고 사각형 모양이 그대로 유지된다고 가정하도록 하겠습니다(실제로는 약간 다르지만). 그리고 변형된 후의 보를 앞쪽에서 봤을 때 윗부분과 아랫부분이 둥그렇게 휘어지겠지만 거의 평평하다고 가정하겠습니다. 결국 사각형의 윗부분은 찌그러지고 아랫부분은 늘어나면서 아래 그림과 같은 사다리꼴이 만들어집니다.

 

휩응력을 완전 탄성체처럼 가정하면 사다리꼴처럼 변형될 것이다.

 

따라서 휨응력을 받는 부분은 완전 탄성체처럼 입체적으로 힘을 받는다고 가정해볼 수 있습니다 중심에서 위로 갈수록 누르는 힘(압축력)이 세지고 아래로 갈수록 잡아당기는 힘(인장력)이 커집니다. 사각형의 맨 위쪽이 가장 많이 찌그러지고 맨 아래쪽이 가장 많이 늘어납니다.

 

맨 아래에서 맨 위쪽까지 직선처럼 변형된다고 가정하면 가운데 부분에는 늘어나지도 않고 줄어들지도 않는 부분이 있는데, 이 부분을 중립축이라고 합니다. 중립축을 기준으로 바깥쪽으로 갈수록 변형이 선형적으로 커진다면, 응력도 마찬가지로 선형적으로 증가한다고 볼 수 있습니다. 맨 위쪽에 최대압축응력이 발생하고 맨 아래쪽에 최대인장응력이 발생합니다.

 

단면2차모멘트라는 개념이 필요한 것은 보와 같이 휘어지는 부재 단면의 성능을 평가하기 위해서입니다. 모멘트는 힘과 거리의 곱으로 나타나는데, 위 그림에서 볼 수 있는 것처럼 휨모멘트가 발생하는 부재는 중립축에서 멀어질수록 거리에 증가하면서 압축응력이나 인장응력이 커지기 때문에 거리에 따른 영향이 제곱, 즉 거리의 제곱의 형태로 나타나게 됩니다.

 

이전 글에서 살펴본 단면1차모멘트는 미소단면과 거리의 곱으로 계산한 것이 때문에 미소단면과 거리의 제곱으로 계산한 값이 필요한 것입니다. 자 이것을 자세히 살펴보겠습니다.

 

단순보의 휨변형

만일 단순보의 양단을 구부리면 다음 그림과 같이 변형될 것입니다.

 

 

위 그림처럼 보의 축방향을 x축으로 하고 그것에 직각인 방향을 y축이라고 할 때 보의 축(도심을 연결한 선)이 변형된 후의 곡선을  y=v(x)와 같이 나타낼 수 있는데, 이 곡선을 처짐곡선(또는 탄성곡선)이라고 합니다. 이 처짐곡선의 y값이 변형이 됩니다. 

 

위 그림에서 보의 좌측단 o에서 x만큼 떨어진 위치가 A지점이라고 할 때 이 미소부분을 확대하면 다음과 같이 됩니다. 

 

 

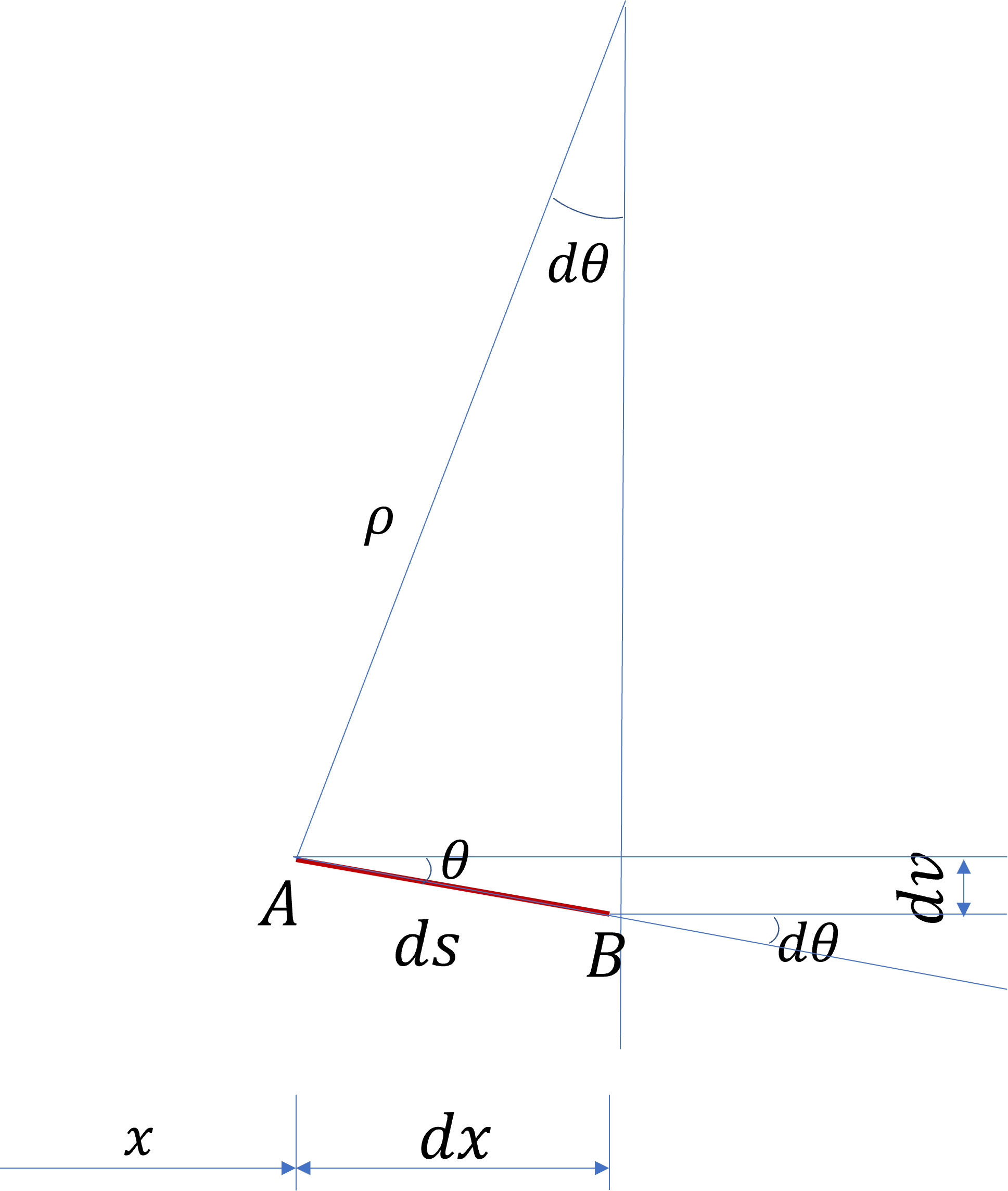
A점에서 처짐곡선의 접선과 x축 사이의 각도를 처짐각이라고 하고 Θ라고 표기하겠습니다. A점에서 x좌표를 따라 미소 거리 dx만큼 떨어진 지점을 B라고 하겠습니다. 이때 처짐량의 증가분을 dv라고 하면 처침각은 다음과 같이 나타낼 수 있습니다. 

 

한편 A점에서의 법선(접선에 직각)과 B점의 법선이 한 점에서 만나게 되는데, 이 교차하는 법선의 각도가 d Θ가 됩니다. 

또한 이 교점과 중립축까지의 거리를 곡률반경이라고 하고 ρ라고 표기하겠습니다. 만일 ds가 충분히 작다면 AB의 거리는 반경 ρ의 호라고 볼 수 있습니다. 이 경우 다음과 같이 나타낼 수 있습니다. 

 

 

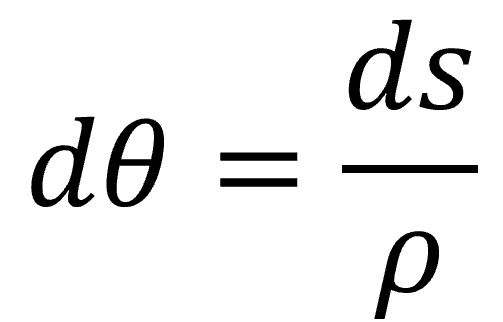
여기서 곡률반경( ρ)은 곡률(Φ)의 역수이고, 처침량의 증분 dv이 충분히 작다면 다음과 같이 나타낼 수 있습니다.

 

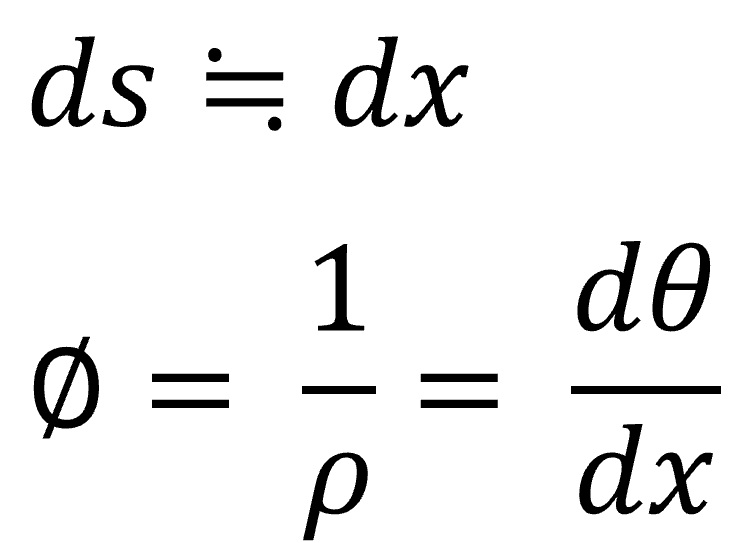
따라서 두 식을 다음과 같은 식을 도출할 수 있습니다. 이

 

보의 휨응력도(휨모멘트에 의한 단면의 응력도)

보에 하중이 작용하면 휨모멘트가 발생하고 단면은 아래 그림과 같이 사다리꼴처럼 변하게 됩니다. 이때 단면에 발생하는 응력도를 살펴보겠습니다.

 

 

응력도를 따질 때는 모형을 단순화하기 위해 평면이 유지된다고 가정하겠습니다. 이 때 중립축으로부터 y만큼 떨어진 지점의 변형량은 그림과 같이 ydΘ가 됩니다. 따라서 이 지점의 변형도는 ε= yd Θ /dx = Φy가 됩니다.

후크의 법칙, 즉 탄성계수는 E = σ/ ε  이므로 다음과 같이 나타낼 수 있습니다.

 

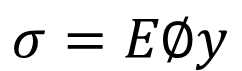
이 수직응력도를 휨응력도라고 합니다.

 

실제로 단면 상에 발생하는 휨응력도는 선형으로 변화하지는 않지만, 미소단면적 dA는 거의 0에 가깝다고 본다면 그 변화량을 무시해도 된다고 볼 수 있습니다.

따라서 중립축 부근에 발생하는 미소단면의 휨응력도때문에 발생하는 모멘트는  σ ydA라고 할 수 있고, 이 휨응력도는 전단면에 걸쳐 발생하기 때문에 전체 단면의 휨응력도때문에 발생하는 모멘트의 합계는 다음과 같이 나타낼 수 있습니다. 이것은 휨모멘트의 크기와 같습니다.

 

이 식에서 I를 중립축에 대한 단면2차모멘트라고 합니다.

 

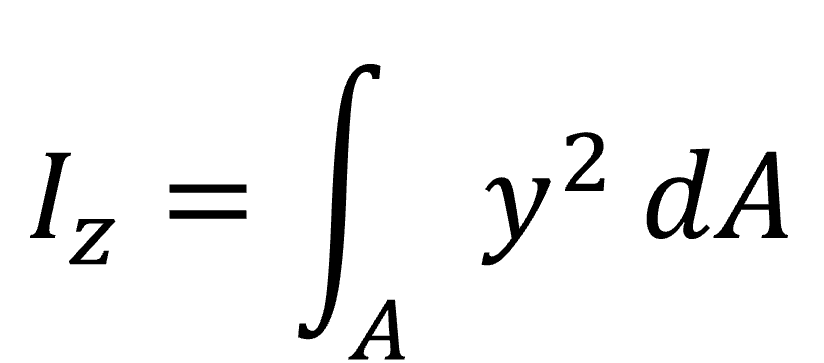
단면2차모멘트와 모멘트는 다음과 같은 관계가 있습니다.

 

단면2차모멘트

앞에서 본 바와 같이 단면2차모멘트는 다음과 같이 나타낼 수 있습니다. 

 

 

따라서 단면2차모멘트의 단위는 길이의 4제곱으로, mm²이 됩니다. 또한 단면2차모멘트는 제곱을 적분한 값이기 때문에 항상 양수값을 나타내게 됩니다. 단면2차모멘트의 계산과정을 다시 한 번 살펴보겠습니다. 

 

 

위 그림에서 오른쪽 그림과 같이 좌표축이 도심에서 떨어져 있을 경우 단면2차모멘트는 다음과 같이 계산할 수 있습니다. 

 

 

 

 

여기서 도심주변의 단면1차모멘트 Sx와 Sy는 값이 0이기 때문에 위 식은 다음과 같이 간단하게 나타낼 수 있습니다. 

 

 

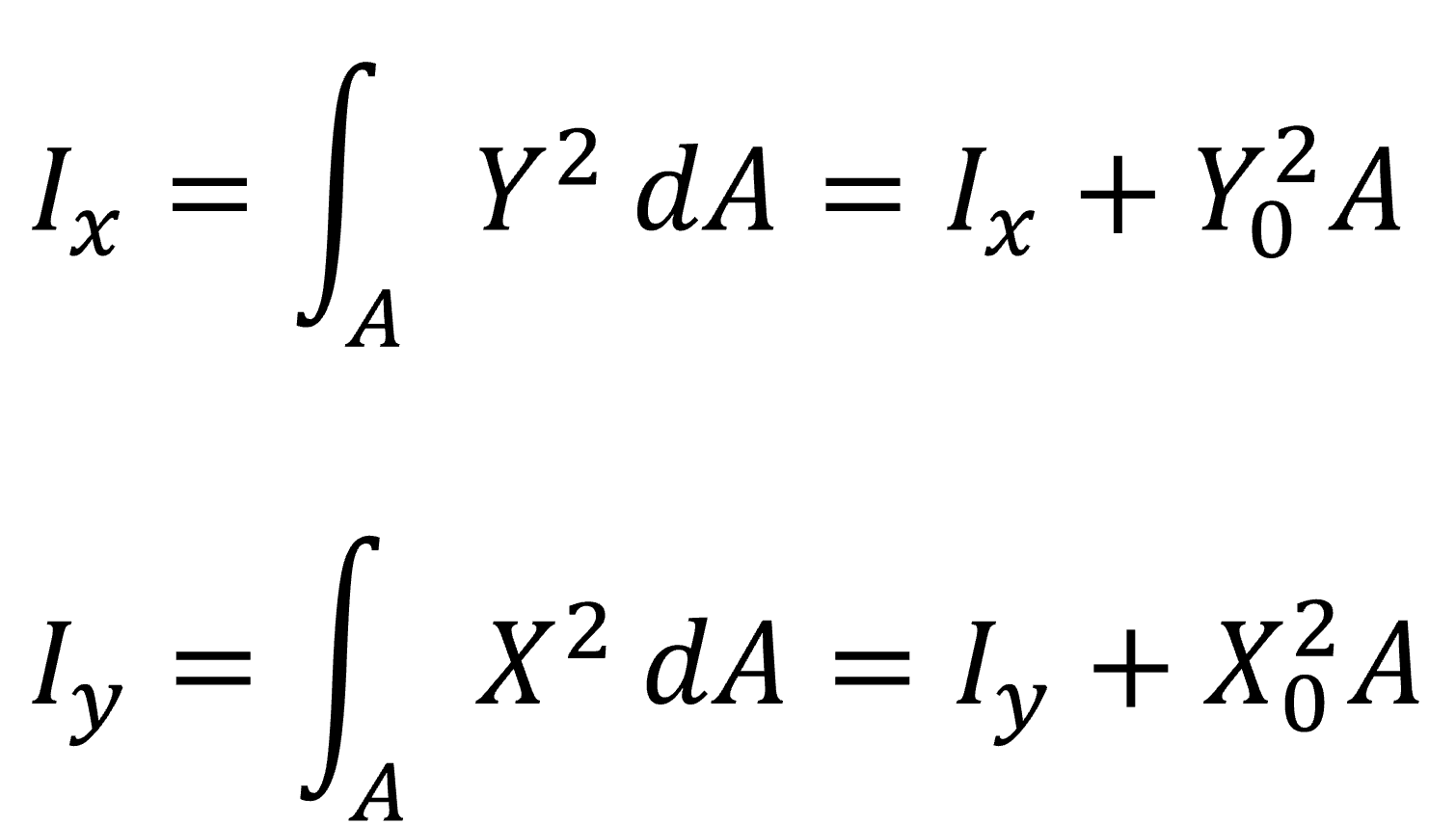
좌표축이 도심으로부터 떨어져 있을 경우 단면2차모멘트값은 도심주변의 단면2차모멘트값과, 도심으로부터 떨어진 직교좌표계의 거리의 제곱과 단면적과의 곱을 더하는 식으로 계산할 수 있습니다. 따라서 단면의 도심에서 멀리 떨어질수록 단면2차모멘트값을 커지는 것을 알 수 있습니다. 

 

다음 그림과 같은 4각형 단면의 x축에 대한 단면2차모멘트를 구해보겠습니다.

 

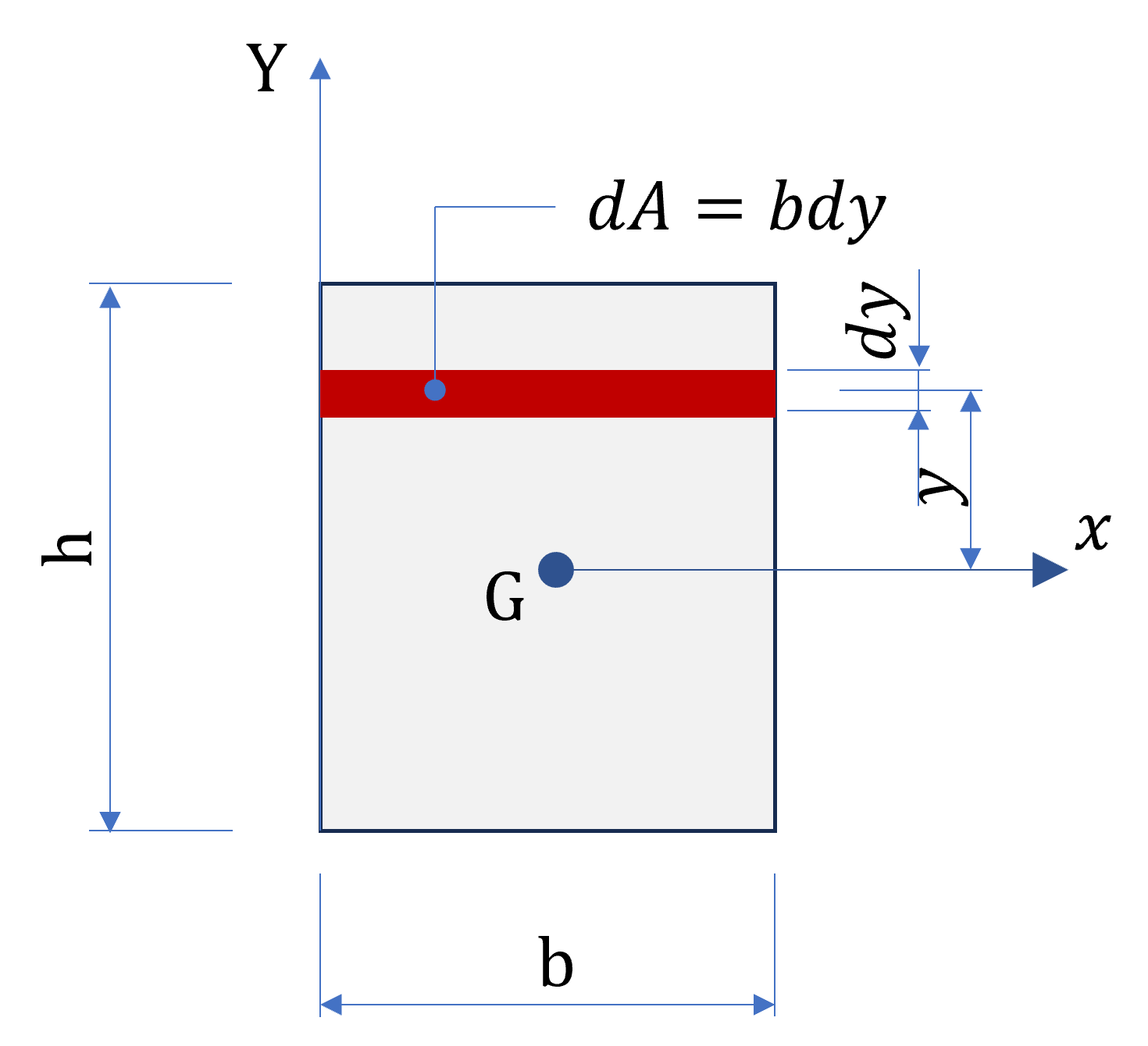
공식을 적용해서 풀면 다음과 같이 됩니다.

 

대표적인 단면의 단면2차모멘트값은 다음과 같습니다. 

 

 

 

▶다음글  모멘트와 단면계수

▶ 단면2차모멘트, 평행축의 정리, 단면극2차모멘트, 단면상승모멘트

 

■ 구조역학 관련 전체 내용 보기

■ 건축 지식 저장소 전체 내용 보기