상세 컨텐츠
본문
앞에서 정정구조물의 응력에 대한 기본적인 개념을 살펴보았습니다. 여기서부터는 정정구조물에서 발생하는 응력을 어떻게 계산하는지 실제로 살펴보겠습니다. 응력은 단면력이라고도 하면 전단력과 휨모멘트를 구해보겠습니다.
■ <이전 글> 정정구조물의 응력 개념
▶ 응력이란?
응력 계산 순서
부재의 응력을 계산하기 위해서는 먼저 지점의 반력을 구해야 합니다.
그런 다음 응력을 계산하는데 필요에 따라서는 구간을 나누어서 응력을 계산할 필요가 있습니다. 다음 그림과 같은 구조물이라면 집중하중을 기준으로 왼쪽과 오른쪽을 나누어서 계산할 필요가 있습니다.

응력을 계산하기 위해서는 잘려진 단면에 생기는 응력의 방향을 먼저 가정합니다. 축방향력과 전단력은 양(+)의 방향으로 가정합니다. 축방향력은 위쪽방향, 전단력은 단면을 시계방향으로 회전시키는 방향이 양의 방향입니다. 휨모멘트는 보 하부에 인장력이 발생하는 방향으로 가정합니다.
▶ 정정구조물의 응력 개념(단면력) <-- 단면력의 부호를 표시하는 방법 참고
응력을 계산할 때는 일반적으로 왼쪽에서부터 계산합니다. 그러나 구간을 나누거나 계산의 편의를 위해서 오른쪽에서 부터 계산하는 경우도 있는데, 이 때는 부호의 방향에 주의해야 합니다.
응력을 계산하기 위해서는 3개의 평형식을 이용합니다. 평형식을 이용해서 계산한 결과값이 양수이면 처음에 가정했던 응력의 방향이 일치한다는 뜻이며, 음수일 경우에는 방향이 반대라는 것을 의미합니다.
마지막으로 응력도를 그립니다. 분포하중이 작용할 경우에는 휨모멘트 다이어그램이 2차함수의 형태가 됩니다. 전단력은 휨모멘트의 도함수이기때문에 휨모멘트의 변곡점은 전단력이 0이 되는 지점이 됩니다.
응력 계산 실례
위 그림과 같은 단순보에 집중하중이 작용할 때 보 부재에 응력이 어떻게 나타나는지 살펴보겠습니다.
1. 반력 계산
다음과 같이 반력을 가정한 후 반력을 구해보겠습니다.
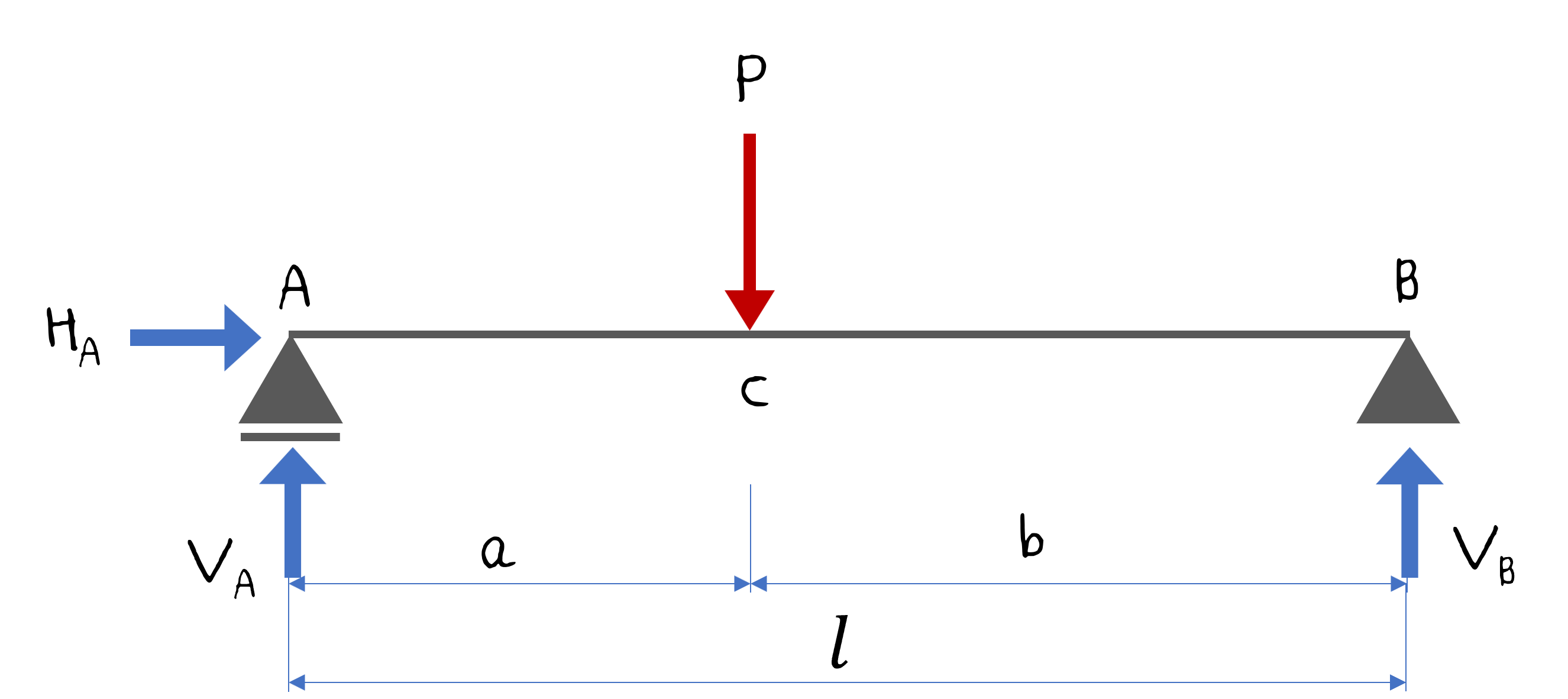
반력을 가정한 후 3개의 평형식을 이용해서 반력을 구하면 다음과 같이 됩니다.

2. 응력 계산
이 부재는 구간을 나누어 계산해야만 합니다. 따라서 먼저 AC구간에 해당하는 부재를 잘라서 나타내면 다음과 같이 됩니다.

이렇게 잘라낸 부재에서 3개의 평형식을 이용하면 다음과 같이 계산할 수 있습니다.


이렇게 해서 C점에서의 모멘트까지 구할 수 있습니다.
AC구간에 대해 구한 다음에는 CB구간을 구하면 되는데, 왼쪽부터 구한다면 다음 그림과 같이 약간 복잡해집니다.

그래서 다음 그림과 같이 오른쪽에서 풀어내는 것이 조금 더 쉽습니다.
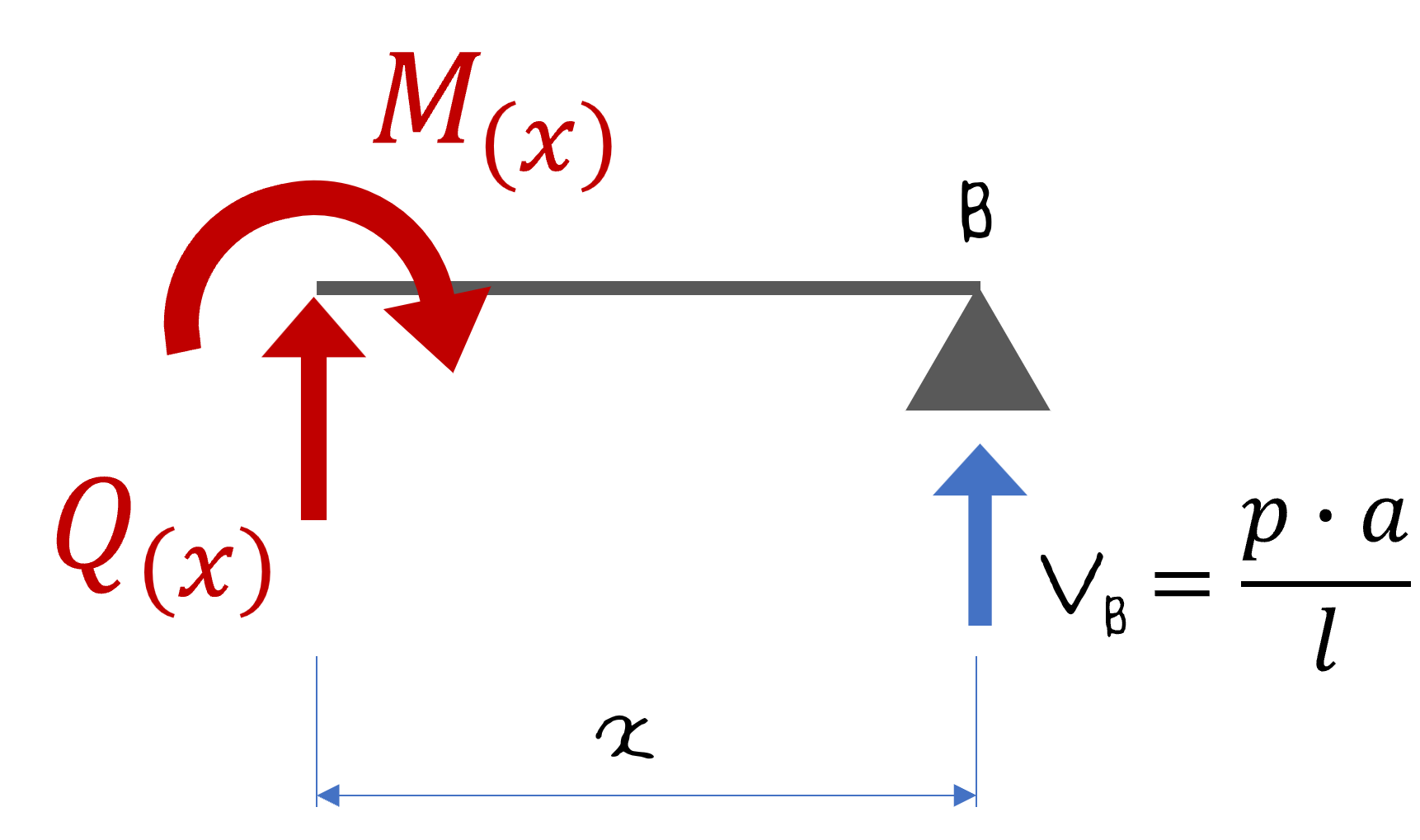
위 그림처럼 오른쪽에서 잘라낸 부재에 대해 3가지 평형식을 이용해서 구하면 다음과 같이 계산할 수 있습니다.

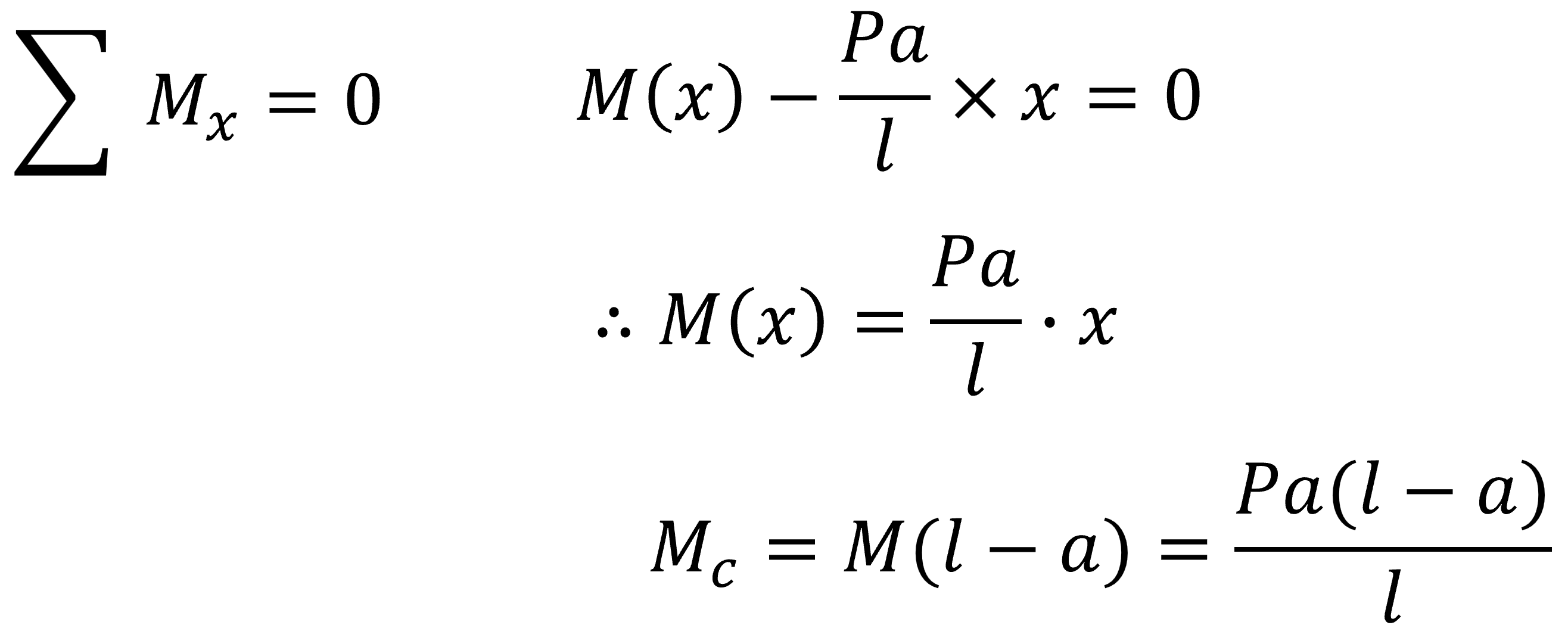
이렇게 모든 구간의 부재에 대해 전단력과 휨모멘트를 구했으면 다음과 같이 전단력도과 휨모멘트도를 그릴 수 있습니다.
전단력도(SFD; Shearing Force Diagram)
전단력도는 영어의 앞글자를 따서 SFD라고도 하며, 전단력도를 그릴 때는 보통 가로방향으로 부재축을 기준으로 위쪽에 양(+)의 전단력을 표시하고, 아래쪽에 음(-)의 전단력을 표시합니다. 따라서 위와 같이 집중하중 P가 작용하는 단순보는 A-C구간은 양의 전단력이 되고, C-B구간은 음의 전단력값이 나타나게 됩니다.

휨모멘트도(BMD; Bending Moment Diagram)
휨응력도는 영어의 앞글자를 따서 BMD라고도 하며, 휨모멘트도를 그릴 때는 보통 부재축을 기준으로 아래쪽에 양(+)의 휨모멘트를 표시하고, 아래쪽에 음(-)의 휨모멘트를 표시합니다. 이렇게 표시하면 부재가 휨모멘트를 받아 늘어나는 쪽에 휨모멘트를 표시할 수 있어 철근의 주로 배근되어야 하는 곳을 알기 쉽게 나타낼 수 있습니다.
위와 같이 집중하중 P가 작용하는 단순보에서는 집중하중이 작용하는 C점에서 가장 큰 휨모멘트가 나타나는 것을 알 수 있습니다.

■ <다음 글> 캔틸레버보(정정구조물)의 응력 계산
'구조역학 > 정정구조물의 응력' 카테고리의 다른 글
| 보의 처짐곡선/ 처짐각/ 휨응력도와 단면2차모멘트 (0) | 2024.01.28 |
|---|---|
| 캔틸레버보(정정구조물)의 응력 계산 (2) | 2024.01.26 |
| 휨모멘트와 전단력의 관계(응력 개념) (0) | 2024.01.25 |





