좌굴의 기본 개념/ 좌굴 안정성

기둥과 같은 구조물이 중심 축하중을 받을 때 압축력이 한계치보다 작으면 변형이 발생하지 않고 원래의 형태를 유지하는데, 어느 한계를 넘어서면 옆으로 구부러지게 되고 이것을 좌굴이라고 합니다. 또한 한계치 하중을 좌굴하중이라고 합니다.

 

임계하중의 기본계산

임계하중을 계산하기 위해 다음가 같은 같단한 구조물을 살펴보겠습니다.

 

중심 축하중을 받는 기둥에서 변형이 발생하고 이때의 처짐각을 θ라고 할 때 B점에서의 모멘트는 다음과 같이 됩니다.

 

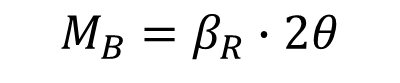
가운데 지점 B에 이상적인 스피링이 있다고 생각하기도 합니다. 이 스프링을 구부리는 원래 상태로 되돌릴려는 힘이 있는데 이것을 휨강성이라고 생각하면 될 것 같습니다. 이 스프링을 구부린 각도가 총 2θ이므로 스프링의 휨강성에 스피링을 구부린 총 각도를 곱하면 모멘트를 계산할 수 있습니다 .

강도와 강성의 차이는 다음 글을 참고하시기 바랍니다.

 

▶ 강도와 강성(탄성계수), 취성과 연성

 

▶ 축방향력 - 강성도와 유연도

 

임계하중을 유도하기 위해 BC 지점만을 연결한 자유물체도를 확대해보면 다음과 같습니다. 

 

구조물의 어느 지점에서도 힘의 평형식은 유지되어야 하기 때문에 B점에서의 총 모멘트의 합은 0이 되어야 합니다. 따라서 다음과 같은 관계식을 얻을 수 있습니다. 

 

 

만일 C점에서의 각도 θ가 매우 작을 경우에는 B 점에서의 변형인 δ 와 다음과 같은 관계가 성립합니다. 

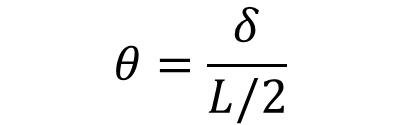
따라서 변형은 다음과 같은 관계식을 얻을 수 있습니다.

 

B점에서의 모멘트 평형식에 변형을 대입하면 다음과 같이 됩니다.

 

여기서 B점에서의 모멘트는 다음과 같은 관계가 있었으므로 이 값을 대입합니다. 

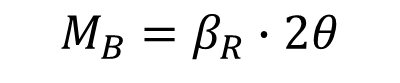
그러면 

 

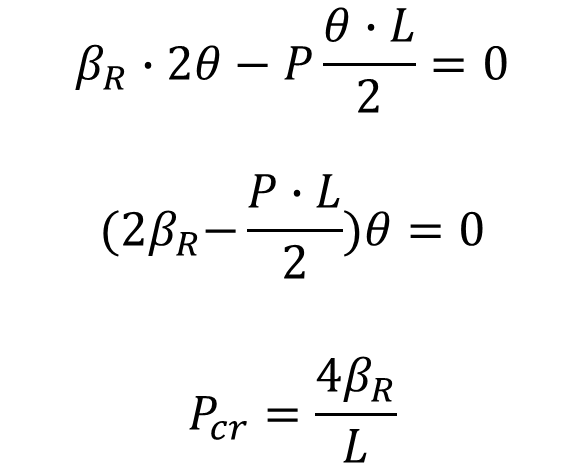
임계하중은 단면의 강성에 비례하고 길이에 반비례하다는 것을 알 수 있습니다.

 

•  P<Pcr일 경우  (축하중에 의한 좌굴 < 모멘트 복원 효과 ) : 하중을 제거하면 모멘트에 의한 복원효과로 다시 원상태로 복원 되므로 안정상태가 됩니다.
• P>Pcr일 경우 (축하중에 의한 좌굴 > 모멘트 복원 효과 ) : 불안정상태가 된다. 

■ 기둥의 좌굴

 

■ 구조역학 관련 전체 내용

구조 부재와 관련된 내용입니다.

■ 슬래브의 종류
■ 슬래브 구조 해석의 원리
■ 슬래브와 수평하중
■ 슬래브 - 주열대와 중간대

 

■ 보의 구조적 역할
■ 보 경간과 춤
■ 보의 처짐과 사용성

 

■ 기둥의 구조적 역할

■ 기둥의 구조설계 - 기둥의 크기를 줄이려면?

 

■ 건축 지식 저장소 전체 내용 보기