상세 컨텐츠
본문
일반적으로 지점의 반력이 3개 미만이 되면 구조물은 불안정하게 되는데, 여기서는 구조물의 안정/불안정, 정정/부정정 상태를 판정하는 방법에 대해 살펴보겠습니다.
■ <이전 글> 구조물 해석을 위한 하중의 종류
구조물의 상태는 구조부재의 단면력의 수(미지수)의 합계와 평형식의 수(식의 수)의 합계를 비교해서 판단할 수 있습니다.
안정/ 불안정
구조물에 작용하는 하중과 반력은 외력에 해당하고, 이 외력에 대해 구조물은 응력으로서 구조물의 내부의 저항력이 발생하게 됩니다. 구조물에 하중이 작용할 때 지점의 반력과 부재내부의 응력으로 안정된 정지상태를 유지할 수 있는 구조물을 안정구조물이라고 합니다. 이와는 반대로 정지상태를 유지할 수 없는 구조물이 불안정구조물이 됩니다. 불안정구조물은 식으로 본다면 힘의 평형식을 세울 수 없고, 하중이 작용하면 구조물이 이동하거나 회전하게 됩니다.
정정(靜定)/ 부정정(不靜定)
안정구조물은 정정구조물과 부정정구조물로 나눌 수 있습니다. 정정구조물은 힘의 평형식만으로 지점의 반력과 부재의 응력을 구할 수 있는 구조물을 말합니다. 단순보(simple beam), 켄틸레버보(cantilever beam), 내민보(overhaning beam), 게르버보(gerber’s beam), 3힌지라멘 등이 정정구조물에 해당됩니다.
부정정구조물은 힘의 평형식만으로는 지점의 반력과 부재의 응력을 구할 수 없는 구조물로서 접합조건이 있어야만 계산이 가능합니다. 부정정구조물을 풀기 위해 필요한 적합조건의 수를 부정정차수라고 합니다.
부재 양절점의 구속조건은 다음과 같이 3가지로 나누어볼 수 있습니다. 강접-강접이 m1개, 강접-회전이 m2개, 회전-회전 m3개가 있는 구조물이 있다고 가정해 보겠습니다.

부재 양절점의 구속조건에 따라 미지수는 달라지지만 평형식의 수는 모두 같습니다. 결국 다음과 같이 나타낼 수 있습니다.

미지수의 개수와 평형식의 개수의 차이를 n이라고 하면 다음과 같이 계산됩니다.
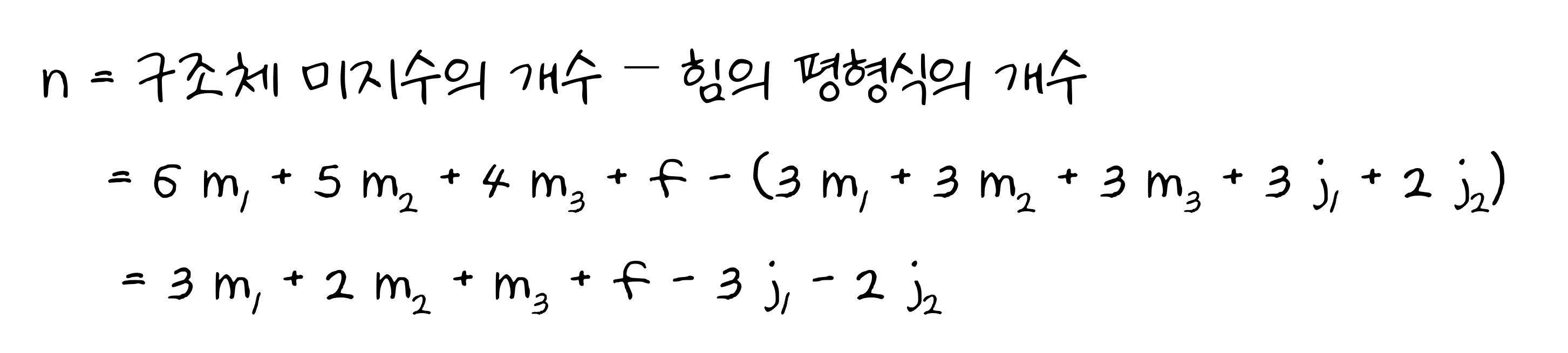
식을 간단히 표현하기 위해서 다음과 같이 단순화할 수 있습니다.

r값은 다음과 같이 계산합니다.
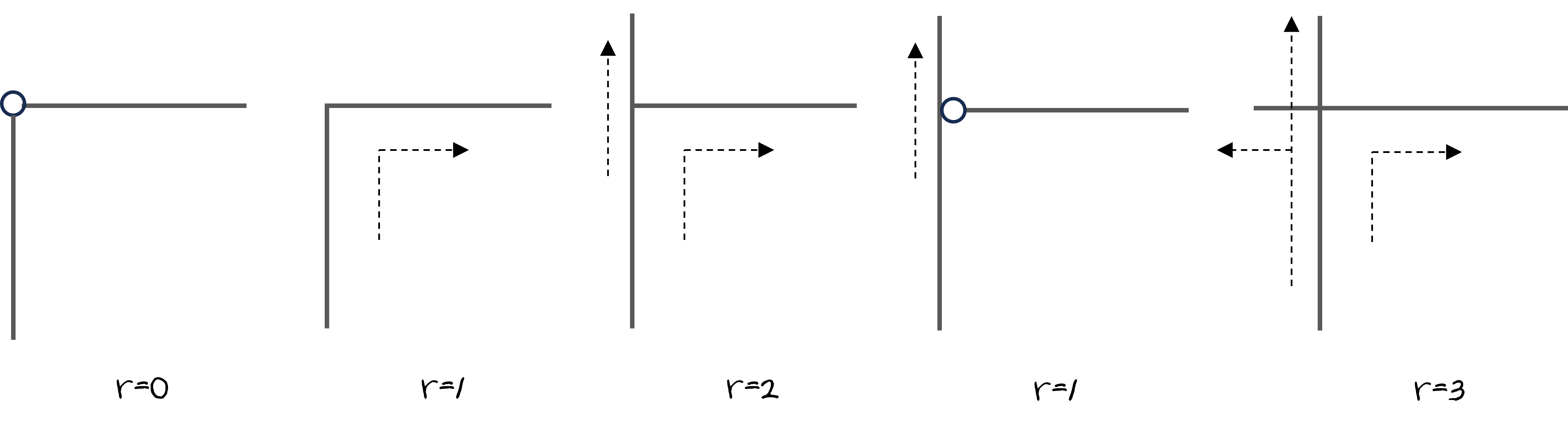
m, j, r을 이용하여 n을 계산하는 식을 정리하면 다음과 같습니다.
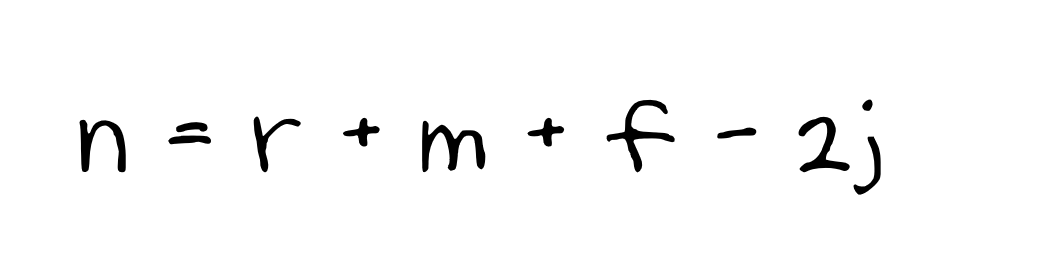
n은 부정정차수로서 다음과 같은 관계가 있습니다.

예제
다음 그림과 같은 구조물의 부정정차수는 어떻게 계산할 수 있을까요?

부정정차수는 다음 식으로 구할 수 있습니다.
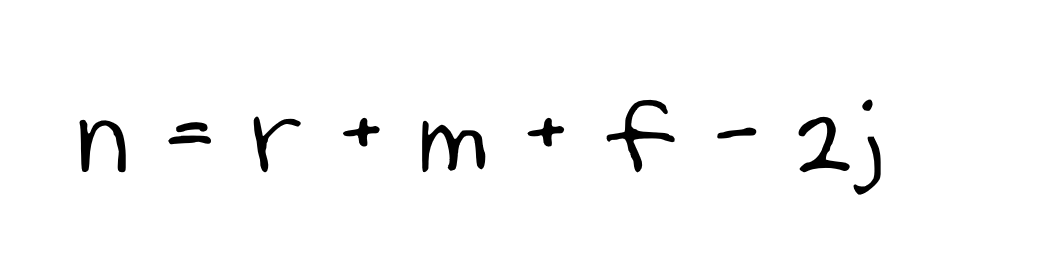
여기서 강절점 개수 r = 2(해설 그림 참조),
부재 개수 m = 5
지점 반력수 f = 9(3 + 3 + 3)
절점 개수 j = 6
n = 2 + 5 + 9 - 2 × 6 = 4 , 즉 4차 부정정
■ <다음 글> 부정정차수 계산/ 부정정구조물/ 간단 해법
■ <다음 글> 정정구조물(보)의 응력 계산
'구조역학 > 부정정구조물' 카테고리의 다른 글
| 부정정차수 계산/ 부정정구조물/ 간단 해법 (1) | 2024.11.14 |
|---|





