상세 컨텐츠
본문
건축구조물에는 다양한 하중이 작용합니다. 그런데 구조물을 해석하려면 이 하중을 계산할 수 있는 방식으로 모델화해야 합니다.
■ 구조물의 모델화와 자유물체도(Free body diagram)
하중의 종류
구조물 해석을 위해 사용하는 하중의 종류는 다음과 같이 3가지 - 집중하중, 분포하중, 모멘트하중-로 나눌 수 있습니다.

관례적으로 사용하는 기호를 보면, 집중하중은 P, 분포하중은 ω, 모멘트하중은 M으로 나타냅니다.
집중하중은 한 지점에 작용하는 힘이기 때문에 단위는 N이나 kN이 되고, 분포하중은 일정한 구간에 등분포로 작용하는 경우 단위 길이당 작용하는 힘의 크기를 나타내기 때문에 N/m 또는 kN/m으로 나타냅니다. 모멘트는 힘과 거리의 곱으로 계산되므로 N·m 또는 k N·m이 단위가 됩니다.
▶ MKS 단위, 힘의 단위(N; 뉴튼)
▶ 우력과 모멘트
예를 들어 보는 슬래브의 하중을 받아 기둥으로 전달합니다. 만약 슬래브가 1방향 슬래브로 설계되어 있다면 작은보가 슬래브의 하중 일부를 큰보로 전달하게 됩니다. 이렇게 슬래브의 하중이 보로 전달될 때 슬래브가 부담하는 분포하중은 아래 그림처럼 나누어져서 보로 전달되고, 작은보의 하중은 집중하중의 형태로 큰보로 전달되게 됩니다.

위 그림을 보면 분포하중의 형상이 다양하다는 것을 알 수 있습니다.
▶ 슬래브의 종류
▶ 슬래브 구조 해석의 원리
힘의 분력
힘은 항상 수직과 수평으로 작용하지는 않습니다. 다음 그림과 같이 직교좌표계에서 경사방향으로 작용할 수도 있습니다.
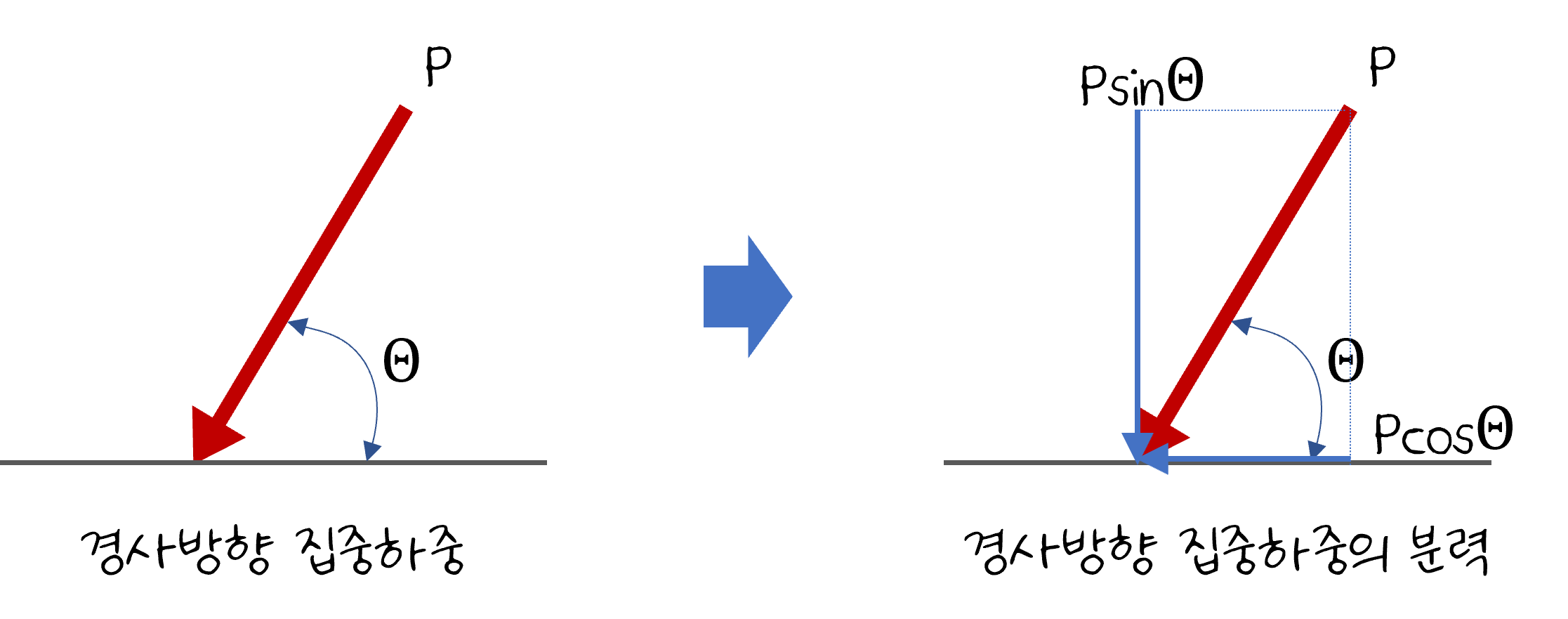
이렇게 하중이 경사방향으로 작용하는 경우 구조물의 반력을 구하려면 경사방향으로 작용하는 하중을 수평방향의 분력과 수직방향의 분력으로 나누어서 계산하는 것이 편리합니다.
▶ 힘의 표현(화살표), 힘의 합성과 분해
캔틸레버보와 등분포하중
아파트 발코니에 동일한 모양의 화분을 골고루 놓아두었다고 가정해보겠습니다. 그러면 발코니 전체에 골고루 하중이 작용하게 됩니다. 건축물에 작용하는 하중이 이런 방식으로 가해지는 것이 보통인데, 이런 하중을 등분포하중이라고 합니다. 즉 집중하중이 연속해서 단위길이당 동일하게 작용하는 것이라고 할 수 있습니다.
이렇게 캔틸레버보에 등분포하중이 가해진다면 다음과 같이 나타낼 수 있습니다.

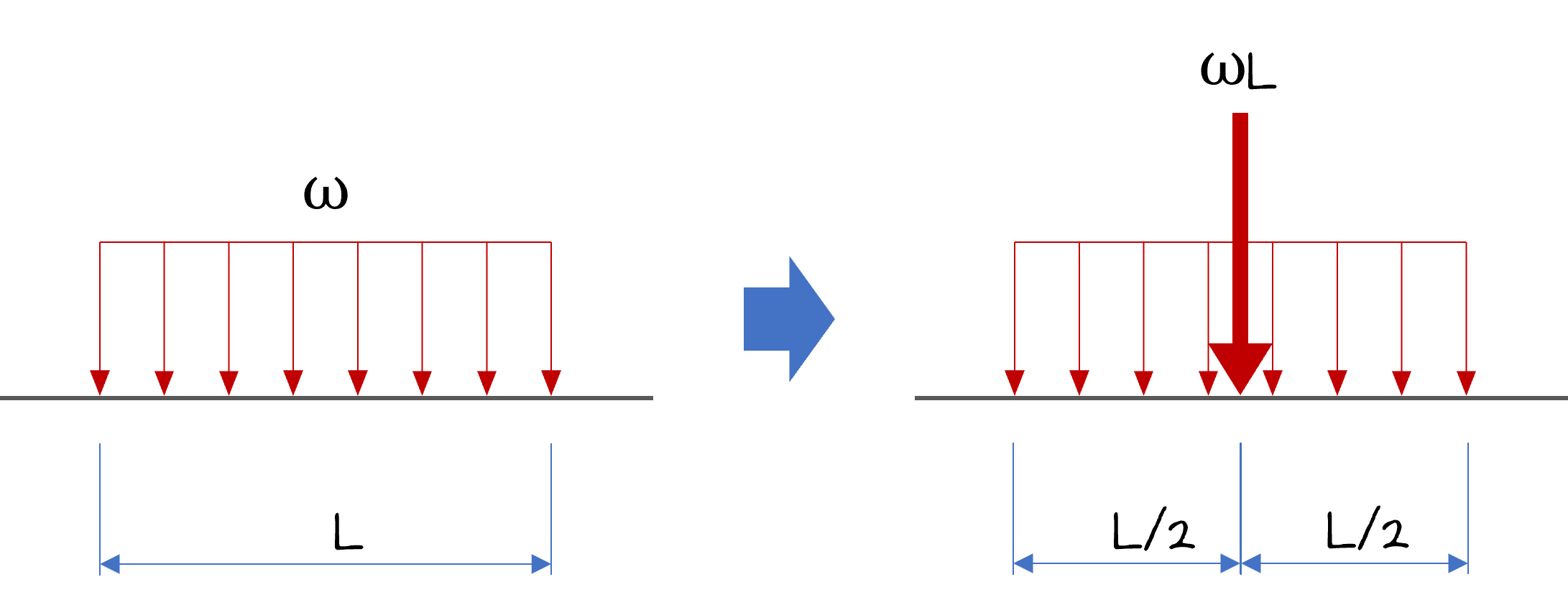
이렇게 등분포하중이 작용할 때 작용하는 반력을 직접 계산하기가 어렵습니다. 그래서 등분포하중을 단순화해서 계산하는데, 다음 그림과 같이 등가의 집중하중이 하중의 중심위치에 합력으로 작용한다고 계산합니다.

그러면 등분포하중이 작용하는 캔틸레버보를 다음과 같이 집중하중으로 치환해서 나타낼 수 있습니다.
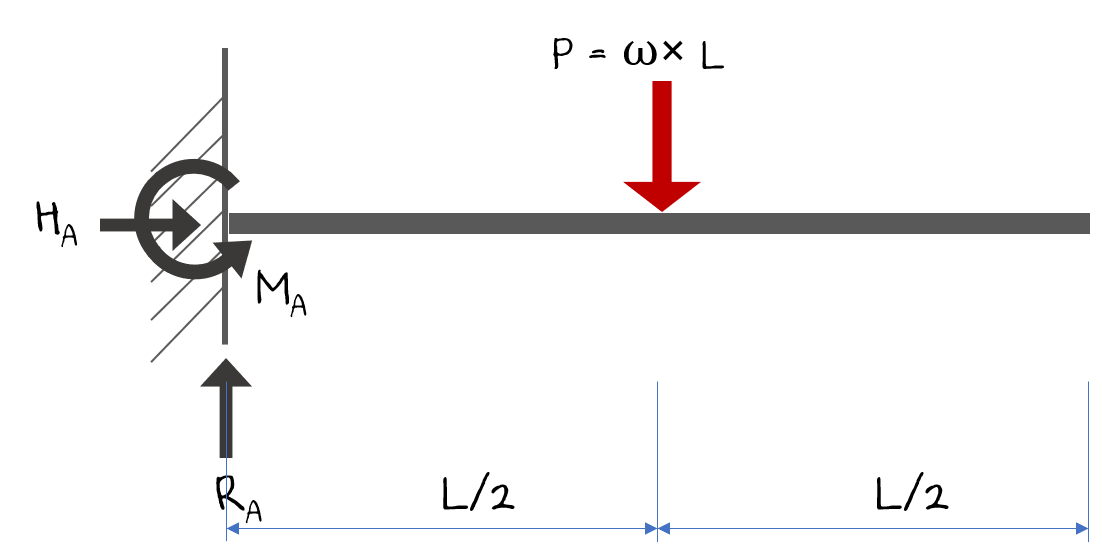
이렇게 분포하중이 작용할 때 지점의 반력을 구하기 위해서는 이 하중을 단순화할 필요가 있습니다. 일정 구간에 작용하는 하중의 전체 합력을 구해서 집중하중의 형태로 작용하는 것으로 단순화시켜서 계산합니다.

구조물의 지점과 절점에 대해서는 다음 글을 참고하시기 바랍니다.
■ <다음 글> 정정구조물의 반력 계산
'구조역학' 카테고리의 다른 글
| 정정구조물의 반력 계산 예제 (0) | 2024.01.21 |
|---|---|
| 정정구조물의 반력 계산 (0) | 2024.01.21 |
| 구조물의 모델화와 자유물체도(Free body diagram) (0) | 2024.01.19 |
| 절점법/ 트러스 부재의 응력 해석 (1) | 2023.05.26 |
| 트러스 부재의 응력 해석/ 절단법/ 프랫 트러스(Pratt truss) (0) | 2023.05.25 |





