상세 컨텐츠
본문
여기서는 힘을 화살표로 표기하는 방법과 다수의 합을 합성하는 방법, 그리고 하나의 힘을 다수의 힘으로 분해하는 방법을 살펴보겠습니다.
■ <이전 글> 힘의 개념/중량과 힘의 차이/스칼라와 벡터
■ <이전 글> 뉴튼, 힘의 단위
힘의 표현
스칼라와 달리 벡터량인 힘은 화살표로 나타냅니다. 힘을 나타낼 때는 3가지 요소-작용점, 방향, 크기-가 필요합니다.
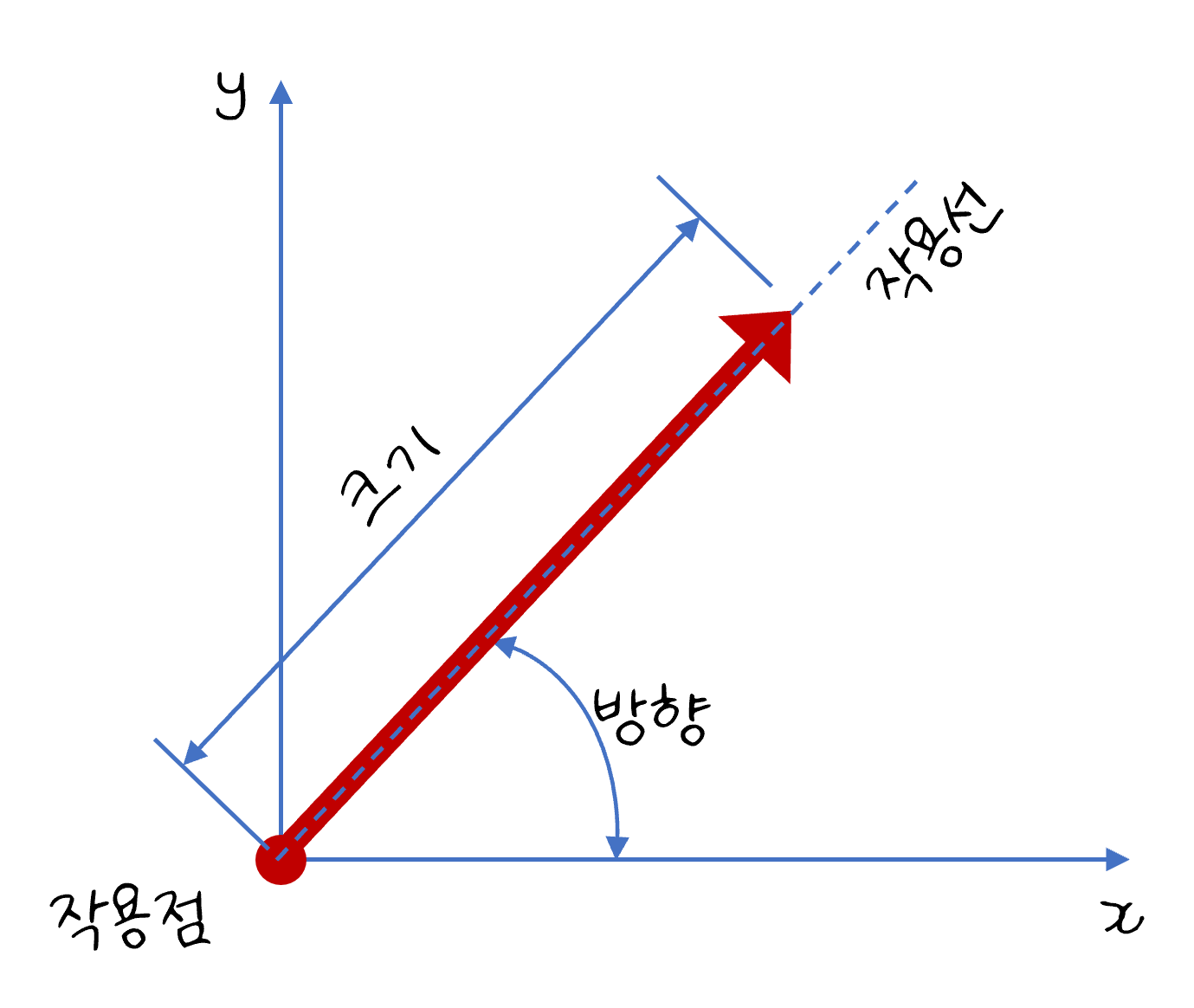
먼저 힘의 작용점을 점으로 표현합니다. 그리고 이 작용점으로부터 힘이 가해지는 방향을 화살표로 나타냅니다. 이처럼 힘은 방향을 가지고 있기 때문에 스칼라와 구분되는 벡터가 되고, 힘을 고려할 때는 반드시 이 방향을 고려해야 합니다.
화살표의 크기는 힘의 크기에 비례해서 나타냅니다.
그림과 같이 공에 줄을 묶어 양쪽 방향으로 당기면 힘을 가하는 방향과 힘이 작용하는 방향이 달라집니다.

▒ 작용선
힘이 작용하는 방향을 ‘작용선’이라고 합니다. 공에 연결된 줄이 하나라면 힘을 가하는 방향과 작용선이 일치하지만, 공을 여러 방향으로 당기면 힘을 가하는 방향과 작용선이 달라지게 됩니다.
힘의 합성
두 방향으로 공을 당기는 힘을 하나의 힘으로 나타내보겠습니다. 이렇게 공을 두 방향으로 당기면 공은 작용선을 따라 움직이게 됩니다. 따라서 이 작용선을 따라 작용하는 하나의 힘으로 합성해서 나타낼 수 있습니다. 이것을 힘의 합성이라고 합니다.
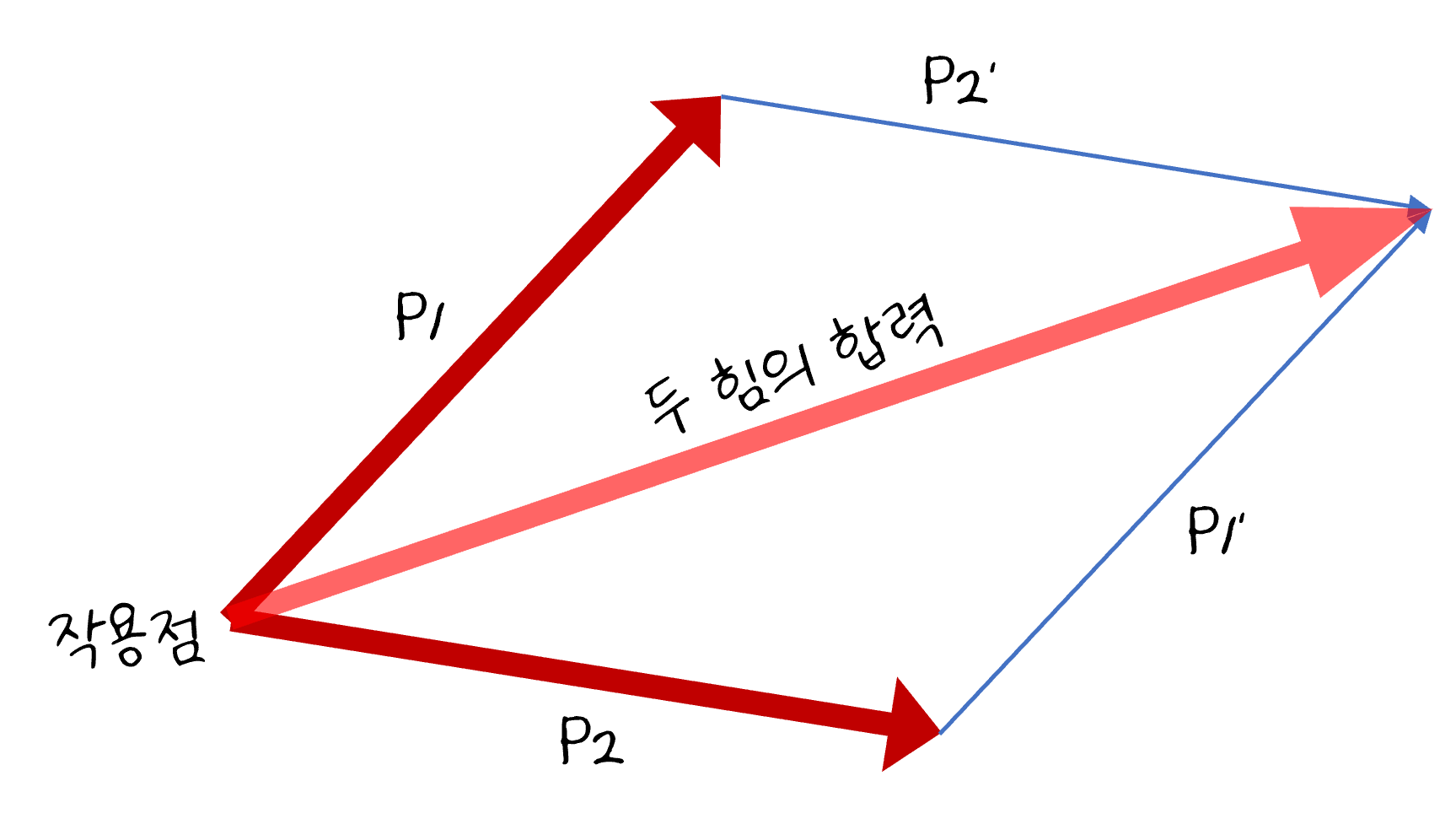
앞에서 나타낸 것처럼 힘을 화살표로 표현하면 힘의 합성을 쉽게 나타낼 수 있습니다. 우선 두 방향으로 당기는 힘을 각각 p1, p2로 해서 화살표로 표현합니다. 이 화살표와 크기와 방향이 같은 선 p1’와 p2’를 상대방 화살표 끝에 그리면 평행사변형을 그릴 수 있습니다. 이제 작용점에서 새롭게 추가한 p1’와 p2’가 만나는 끝점을 화살표로 연결하면 합성된 힘의 크기를 나타낼 수 있습니다.
이처럼 힘을 화살표로 나타내면 여러 힘의 합성 또한 쉽게 나타낼 수 있습니다.
힘의 분해
힘의 합성과 반대로 힘을 분해할 수도 있습니다. 이번에는 하나의 힘을 여러 개의 힘으로 나누는 것입니다.

먼저 힘을 나타내는 화살표P의 작용점이 O에서 분해하고자 하는 방향으로 임의의 크기의 힘을 갖는 P1을 그립니다.
그 다음 두 화살표의 끝을 연결하는 선 BA을 그립니다.
그 다음 작용점 O에서부터 선 BA와 평행한 선을 그립니다. 이 선이 두번째로 분해하는 힘의 방향을 나타냅니다.
A에서부터 BO에 평행한 선을 그리면 교차점인 C가 나오는데, 작용점 O에서 C점을 연결하는 화살표를 그리면 두번째로 분해된 힘 P2를 그릴 수 있습니다.
힘을 합성할 때는 합성한 결과가 1개이지만 힘을 분해할 때는 무수히 많은 방법으로 힘을 분해할 수 있습니다. 또한 분해하는 방법에 분해된 힘이 원래의 힘보다 크게 분해될 수도 있습니다.
경사방향으로 작용하는 힘을 X축과 Y축 두 직각방향으로 분해해서 힘을 다루는 것이 쉽기 때문에 서로 직각방향으로 가장 많이 분해하게 됩니다.
■ <다음 글> 우력과 모멘트
'건축구조 > 힘과 응력' 카테고리의 다른 글
| 축방향력과 변형, 푸아송비 (0) | 2023.01.06 |
|---|---|
| 우력과 모멘트 (0) | 2023.01.04 |
| 구조물의 지점과 절점 (0) | 2023.01.03 |
| 힘의 개념/중량과 힘의 차이/스칼라와 벡터 (0) | 2023.01.02 |
| 휨모멘트와 단면계수 (2) | 2022.08.30 |





