상세 컨텐츠
본문
힘을 화살표로 표현하면 벡터를 효과적으로 표시할 수 있고 합성과 분해도 평행사변형의 법칙을 이용하여 쉽게 할 수 있다는 것을 알 수 있습니다. 그런데 힘의 합성과 분해로 나타내기 어려운 힘의 조합이 있습니다. 바로 우력입니다.
▶ <이전 글> 힘의 표현(화살표), 힘의 합성과 분해
우력
우력(偶力)은 서로 평행하면서 방향이 반대로 작용하는 두 힘을 말합니다.

이렇게 우력이 작용하면 평행사변형의 원리로는 힘을 합성할 수 없습니다. 결국 회전시키려는 힘이 작용하기 때문에 모멘트라는 개념을 도입해서 힘의 작용을 따져볼 수 있습니다.
모멘트
다음 그림과 같이 다이빙 보드에 사람이 서게 되면 다이빙 보드를 아래쪽으로 누르게 됩니다. 그러면 다이빙 보드의 지지점을 중심으로 다이빙 보드를 시계방향으로 회전하게 하는 힘이 작용하게 되는 데, 이렇게 사물을 회전하게 하는 힘을 모멘트(Moment)라고 합니다.

지렛대의 원리를 생각하면 모멘트를 조금 더 쉽게 이해할 수 있습니다. 무거운 물체를 쉽게 들어올리기 위해 우리는 지렛대를 이용합니다. 아래 그림처럼 무거운 물체는 힘의 작용점이 되고, 지점을 중심으로 작용점과 반대되는 쪽을 누르면 무거운 물체는 위로 올라가게 됩니다.

지렛데의 원리는 지점에서 먼 쪽을 누를수록 작은 힘으로 작용점을 움직일 수 있다는 점입니다. 반대로 지점에 가까운 쪽을 누를수록 더 큰 힘을 사용해야 합니다. 운전대를 돌릴 때도 마찬가지입니다. 운전대의 크기가 작다면 더 큰 힘으로 돌려야 하지만, 운전대 크기가 크다면 작은 힘으로 돌릴 수 있게 됩니다.
모멘트는 가해지는 힘의 크기와 지점에서의 거리의 곱으로 나타냅니다.

Moment = Power × Length = P × L
식을 보면 알 수 있는 것처럼 힘의 크기가 크면 클수록, 그리고 지점에서의 거리가 멀면 멀수록 모멘트가 크게 발생합니다.
모멘트의 방향은 시계방향과 반시계방향 두 가지 방향이 있습니다.
우력과 모멘트
그럼 우력은 어떻게 모멘트를 발생하게 할까요? 우력은 방향이 반대이고 서로 평행인 두 힘을 말합니다. 앞에서 살펴본 두 힘은 우력의 중심점을 기준으로 각각 오른쪽(P1)와 왼쪽(P2)으로 작용하는 힘이라고 할 수 있습니다.

이 두 힘의 크기가 각각 10kN이고 두 힘사이의 거리가 3m라고 하면 다음과 같이 모멘트를 계산할 수 있습니다.

이처럼 시계방향으로 회전하는 모멘트를 통상적으로 +로 표기합니다.
편심과 모멘트
다음 그림을 보면 힘P는 점O에서 편심거리 e 만큼 떨어진 지점에 작용하고 있습니다. 이 경우에도 작용점 O에는 모멘트가 발생하는데 모멘트는 힘의 크기와 거리의 곱으로 계산하기 때문에, 이 때 작용하는 모멘트도 M=P·e가 됩니다. 이것을 나타낸 것이 아래에 있는 가운데 그림입니다.
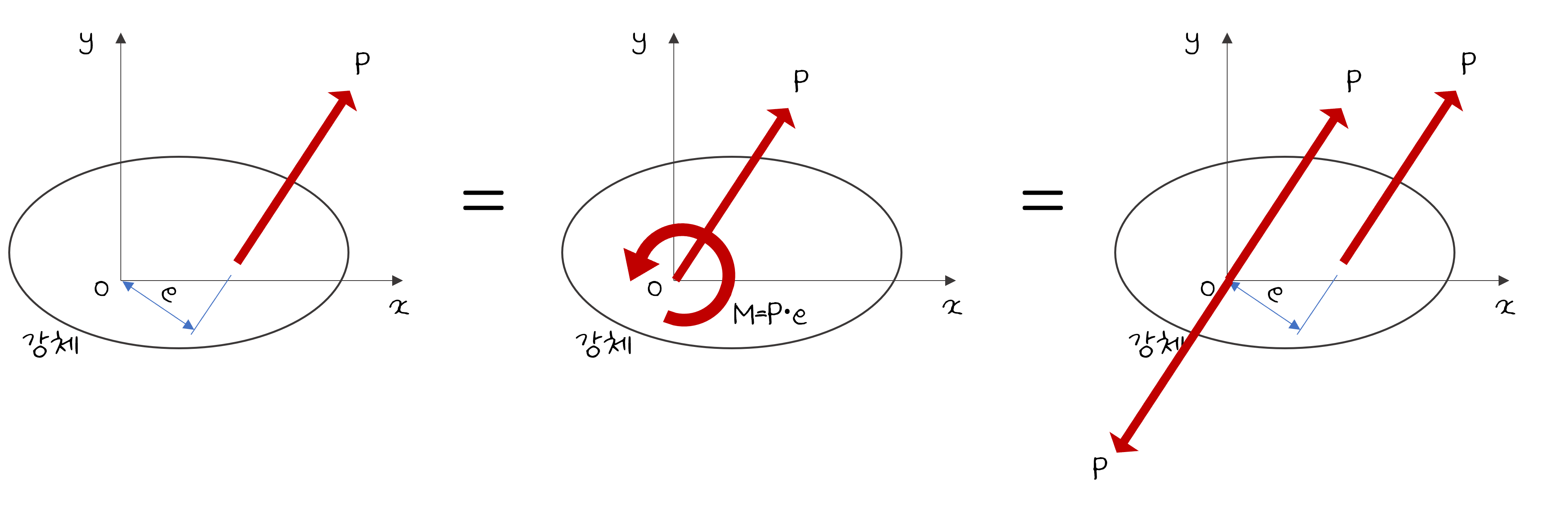
위 그림에서 세번째 그림을 보면 점 O에 힘의 크기가 같고 방향이 서로 반대인 두 힘이 작용하고 있는데, 이 경우 두 힘의 합력은 0이 되므로, 세 그림 모두 같은 개념을 나타낸다고 할 수 있습니다.
다음 그림은 기둥의 중심에서 편심거리 e만큼 떨어진 지점에 힘 P가 작용하는 경우를 나타냅니다. 이 기둥도 앞의 경우와 마찬가지로 도심에 힘 P가 작용하는 것으로 평행이동할 수 있고, 모멘트 M=P·e가 작용하는 것으로 나타낼 수 있습니다.

보에서의 우력
보 부재는 보통 아래로 처지면서 휘기 때문에 원래 사각형 단면이었던 모양이 아래 그림처럼 사다리꼴 모양으로 변하게 됩니다.
■ 휨응력

그래서 중립축에서 위로 갈수록 압축응력이, 아래로 갈수록 인장응력이 커지게 되는데 완전 탄성체로 가정한다면 위 그림 가운데에 있는 것처럼 삼각형 모향으로 힘을 받게 될 것입니다. 그러면 맨 오른쪽에 있는 그림처럼 보의 아래쪽은 인장력이 윗쪽은 압축력이 작용하게 되는데 이 두 힘(우력)에 의해 보가 구부러지는 응력이 발생하게 되는 것입니다.
모멘트는 거리에 비례한다고 얘기했습니다. 결국 보의 두께를 두껍게 만든다면 압축력과 인장력 사이의 중심간 거리를 더 크게 할 수 있고, 보가 모멘트에 저항하는 능력도 더 키울 수 있게 됩니다.
▶ <다음 글> 구조물의 모델화와 자유물체도(Free body diagram)
'건축구조 > 힘과 응력' 카테고리의 다른 글
| 보의 휨모멘트와 처짐 (0) | 2023.01.11 |
|---|---|
| 축방향력과 변형, 푸아송비 (0) | 2023.01.06 |
| 힘의 표현(화살표), 힘의 합성과 분해 (0) | 2023.01.03 |
| 구조물의 지점과 절점 (0) | 2023.01.03 |
| 힘의 개념/중량과 힘의 차이/스칼라와 벡터 (0) | 2023.01.02 |





