상세 컨텐츠
본문
이전에 정정구조물에서 발생하는 응력을 어떻게 계산하는지 살펴보았는데요, 이것은 부재가 선으로 이루어져 있다고 이상화해서 계산한 것입니다. 현실의 모든 부재는 두께가 있지만 선적인 부재로 이상화하면 응력이 한 점에 집중되어 나타난다고 가정한 것입니다. 여기서는 축방향력과 변형에 대해 살펴보겠습니다.
축방향력과 변형
다음 그림과 같은 원통형 물체에 인장력이 가해졌다고 가정해보겠습니다. 원래 원통은 원통의 지름이 D이고 길이가 L이 원통이라고 가정하겠습니다.

이 원통에 인장력 P가 작용하면 어떤 사물이든 늘어나게 됩니다. 이렇게 늘어나는 양을 ΔL이라고 하면 늘어난 전체 길이는 L + ΔL이 되겠죠? 만일 압축력이 작용한다면 길이가 줄어들게 될 것입니다.
이렇게 어떤 물체에 외력이 작용하면 이 외력에 대응하기 위해 내부에서는 응력이 발생합니다. 외력에 대해 내부에서 발생하는 이 저항력을 응력이라고 할 수 있습니다.
■ 응력이란?
▒ 응력도(δ)
축력이 작용하면 부재 내부 단면에 발생하는 응력은 매우 단순하게 나타나고(Uniform stress distribution), 원통형 내부에 있는 입자들은 서로 비슷하게 늘어나는 힘을 받는다고 가정할 수 있습니다.
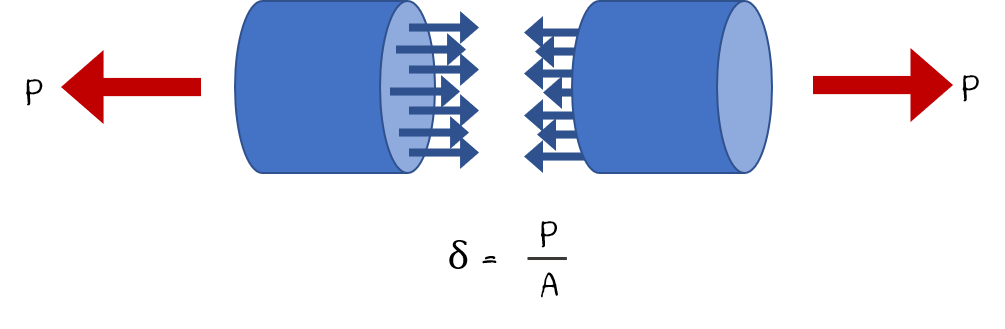
이 응력을 보통 δ로 표기하는데 이 응력은 보통 단위면적당 힘의 크기로 나타내기 때문에 축방향력을 단면적으로 나누어서 표기합니다. 따라서 δ = P/A가 됩니다.
▒ 변형도(ε)
그리고 재료가 변형이 되는 정도는 원래의 길이에 영향을 받게 됩니다. 즉 기다란 고무줄을 잡아당기면 많이 늘어나고 잛은 고무줄을 당기면 조금 늘어납니다. 따라서 어떤 재료든 단위길이당 어느 정도 늘어나는가로 비교하는 것이 타당합니다. 이것을 변형도라고 하고 보통 ε로 표기합니다. 이 변형도는 늘어난 길이를 원래의 길이로 나누어서 나타냅니다.
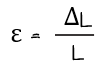
▒ 응력-변형도곡선
어떤 재료를 구조재료로 사용하려면 축방향력이 작용할 때 변형도가 어떻게 나타나는지, 쉽게 말해서 힘이 가해졌을 때 얼마나 변형되는지를 알아야만 합니다. 그래서 우리는 응력도와 변형도의 관계를 그래프로 그려서 나타냅니다.
▶ 응력-변형도 곡선이란?
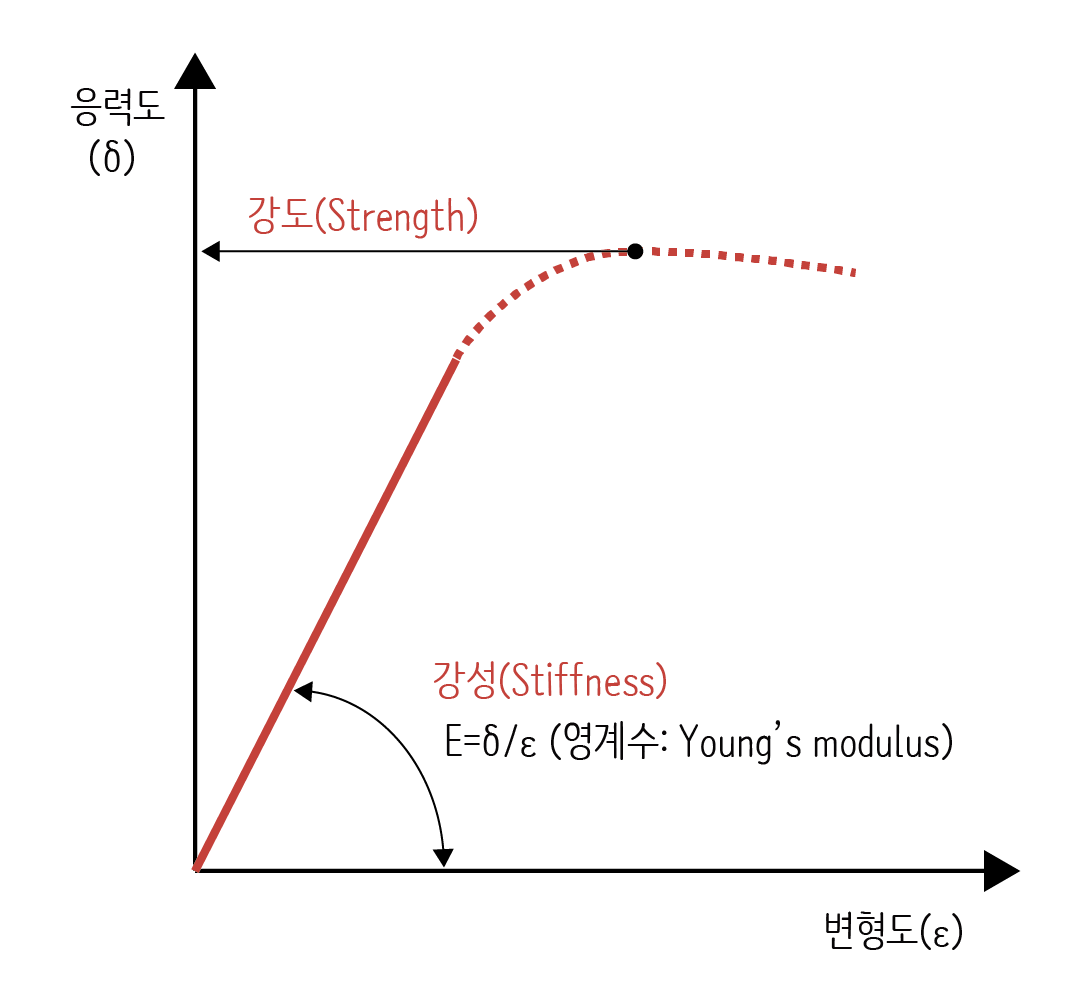
어떤 재료의 응력도와 변형도의 관계를 그려보면 다양하게 나타나지만 대부분 응력이 작은 영역에서는 위 그림처럼 직선적인 관계가 나타납니다. 그래서 이 기울기가 재료의 변형을 이해하는데 매우 중요한 역할을 합니다. 응력 - 변형도 곡선에서 변형에 저항하는 능력은 직선의 기울기로 파악합니다. 이 기울기를 탄성계수(Modulus of elasticity)라고 하는데 영국의 과학자 토마스 영(Thomas Young, 1773 ~ 1829)의 이름을 따서 영계수(Young's modulus)라고도 합니다.
■ 강도와 강성(탄성계수), 취성과 연성
그래프를 보면 알 수 있듯이 이 탄성계수는 응력도를 변형도로 나눈 값입니다.
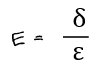
이 식은 변형하면 응력도를 다음과 같이 표기할 수 있습니다.
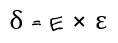
앞에서 응력도와 변형도를 어떻게 계산하는 것인지 서술했으니, 그 식을 대입해보면 다음과 같습니다.
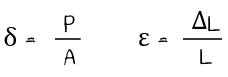
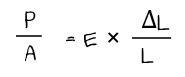
자 그럼 축방향력이 작용할 때 변형이 얼마나 발생하는지 쉽게 계산할 수 있겠죠? 위 식을 변형하면 다음과 같이 됩니다.

위 식을 보면 축방향력이 클수록, 길이가 길수록 선형적으로 비례해서 변형이 커지는 것을 알 수 있습니다. 반대로 탄성계수가 크거나 단면적이 크면 그만큼 변형에 저항하는 능력이 커져서 변형도 작아지는 것을 알 수 있습니다.
푸아송비
여기서 축방향력이 작용할 때의 재료가 어떻게 변형되는지 조금 자세히 들여다 보겠습니다.

위 그림에서 본 것처럼 인장력이 작용할 때 재료가 늘어나게 되는데 두께는 반대로 얇아지는 것을 알 수 있습니다.
봉재에 힘이 작용하면 변형되는데 질량불변의 법칙에 따라 인장력이 작용하면 단면이 줄어들고 압축력이 작용하면 단면이 커지게 됩니다. 즉 축방향력이 가해지는 축방향의 변형도와 축방향의 직각방향의 변형도가 다르게 나타난다는 것을 알 수 있습니다.
이 때 축방향의 변형도를 x로 나타내면 다음과 같습니다.
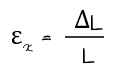
축방향의 직각방향의 변형도를 y로 나타내면 다음과 같습니다.
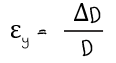
그런데 이 축방향의 변형도와 횡방향의 변형도가 재료마다 다르다는 것을 발견한 사람이 있습니다. 이 비를 프랑스의 수학자이자 물리학자인 시메옹 드니 푸아송(Siméon Denis Poisson, 1781.6.21~1840.4.25)의 이름을 따서 푸아송 비(Poisson's ratio)라고 합니다.
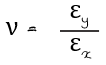
모든 재료는 일정한 포아송비 값을 보이는데 금속류는 0.25~0.35 사이에 위치하고 강재는 대략 0.3를 많이 적용합니다.
콘크리트는 0.1~0.2(주로 0.2), 철근콘크리트는 0.17 정도입니다.
포와송비는 전단탄성계수(G)를 계산할 때 사용됩니다. 전단탄성계수와 포와송비는 다음과 같은 관계가 있습니다.
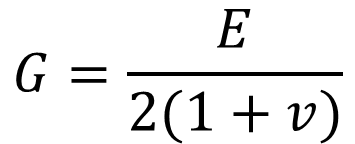
▶ 전단응력
'건축구조 > 힘과 응력' 카테고리의 다른 글
| 반력 계산/ 힘의 평형/ 단순보와 구조역학 (3) | 2023.01.11 |
|---|---|
| 보의 휨모멘트와 처짐 (0) | 2023.01.11 |
| 우력과 모멘트 (0) | 2023.01.04 |
| 힘의 표현(화살표), 힘의 합성과 분해 (0) | 2023.01.03 |
| 구조물의 지점과 절점 (0) | 2023.01.03 |





