단면계수의 의미와 계산 - 탄성단면계수/소성단면계수

이전 글에서 보에서 발생하는 휨모멘트와 단면계수에 대해 말씀드린 적이 있습니다.

 

▶ 휨모멘트와 단면계수

 

일반적으로 보에 휨모멘트가 작용하고 발생하는 휨응력이 탄성구간에 있다면 응력 분포는 다음과 같이 나타나게 됩니다. 여기선 B는 보의 폭, D는 보의 높이가 됩니다. 

 

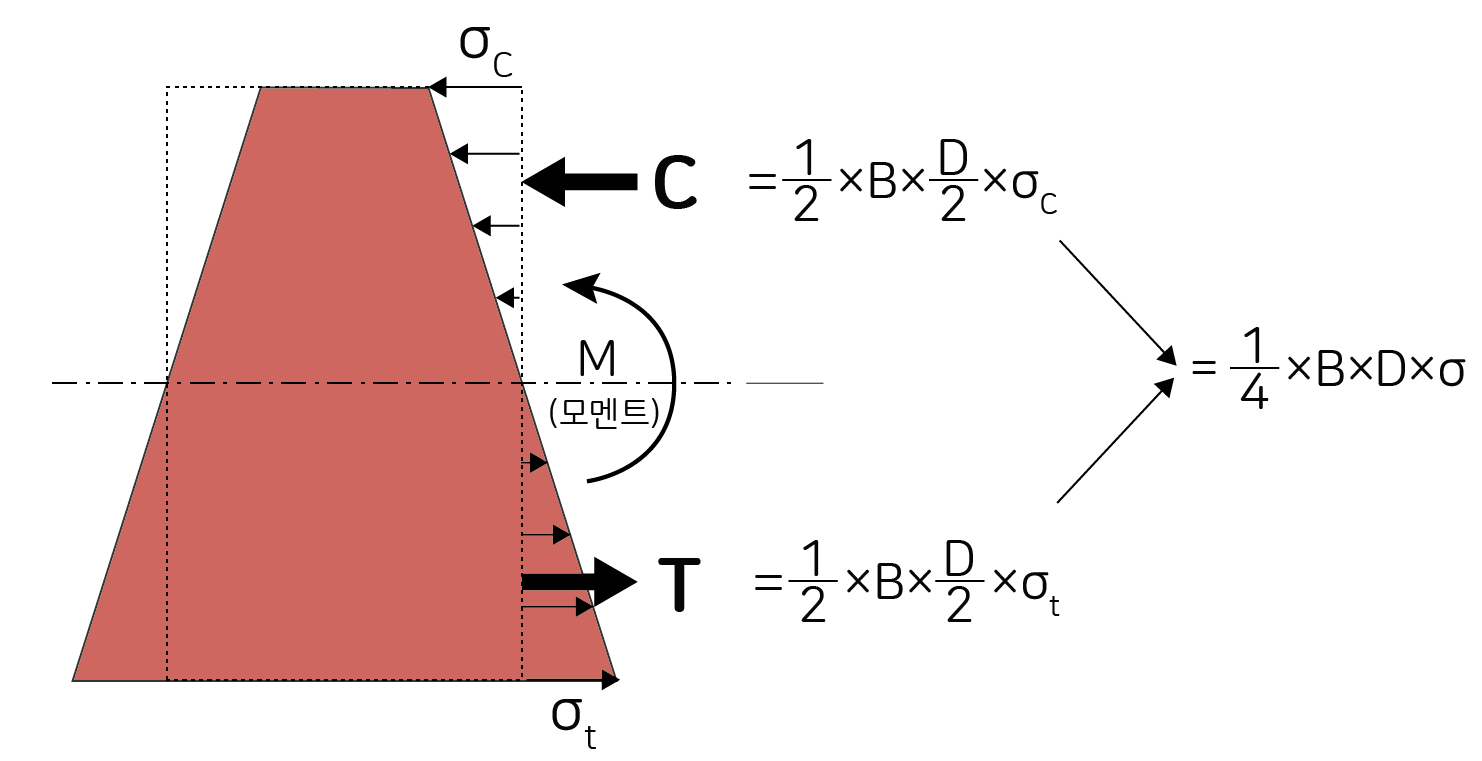
중립축을 기준으로 위쪽으로 갈수록 압축응력이 커지고, 아래쪽으로 갈수록 인장응력이 커지는데, 이 삼각형의 합력은 다음과 같이 됩니다.

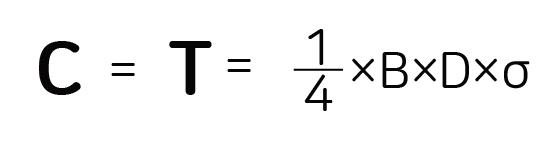
이 C와 T가 보 단면을 돌리는 식으로 작용하니까 모멘트의 크기를 계산하려면 두 힘사이의 거리(j)를 곱해서 계산합니다. 그래서 보에서 발생하는 모멘트는

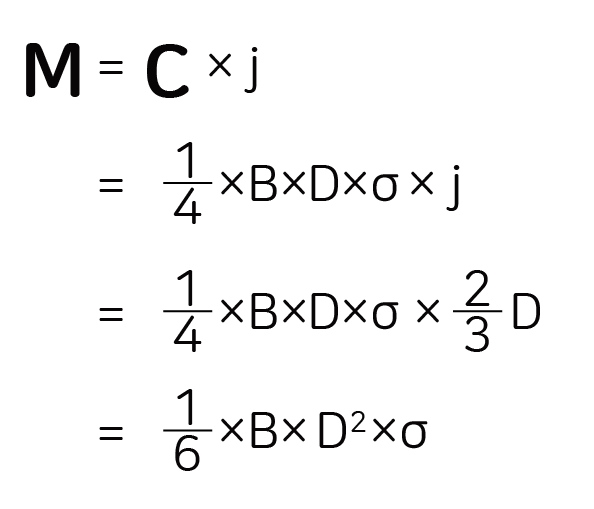
이 식에서 보면 보의 형상과 관련된 부분을 묶어서(다시 말해서 B나 D가 포함된 식을 하나로 묶어서) 나타낼 수 있는데, 이 Z를 단면계수라고 합니다.

 

단면2차모멘트와 단면계수

일반적인 직사각형 단면의 보라고 하면 단면계수는 단면2차모멘트와 다음과 같은 관계가 있습니다.

▶ 보의 처짐곡선/ 처짐각/ 휨응력도와 단면2차모멘트

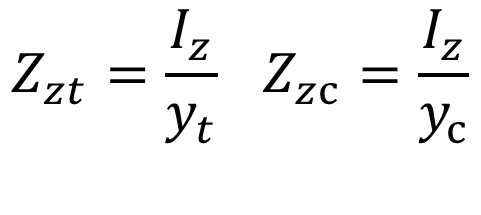
즉 단면계수는 중립축(통상 z축)에 대하여 단면2차모멘트 Iz를 중립축으로부터 단면의 최외단까지의 거리yt (인장측) 또는 yc(압축측)로 나눈 값이 됩니다. 직사각형 단면이라면 중립축에서 단면의 최외단까지의 거리는 h/2 이므로 다음과 같이 됩니다.

 

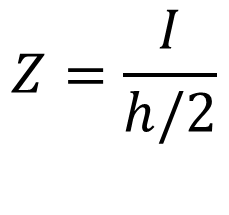
사각형 단면의 단면2차모멘트는 다음과 같이 됩니다.

 

 

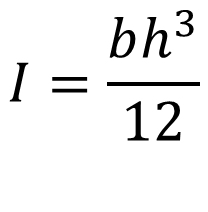
따라서 위 식을 계산해보면 단면계수를 구할 수 있습니다.

 

 

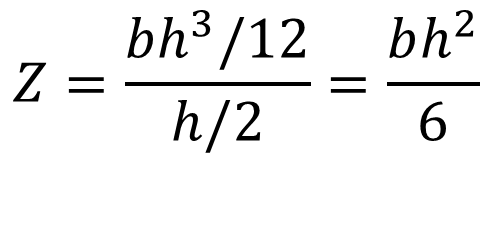
단면계수의 의미

단면계수는 여러가지 의미를 지닙니다. 단면계수를 대입해서 모멘트를 풀어보면 다음과 같이 됩니다.

 

즉 모멘트는 단면계수와 응력의 곱으로 나타내집니다. 거꾸로 예기하면 단면계수가 크면 클수록 모멘트에 저항하는 능력이 커진다는 것이죠. 

 

즉 단면계수는 단면에 발생하는 응력이 1일 때 (단위 응력일 때) 단면이 휨모멘트에 저항할 수 있는 크기라고도 할 수 있습니다. 이런 관계를 이용하면 임의의 응력에 대한 단면의 휨모멘트를 산정하기 위해 단면계수를 이용할 수 있습니다.

 

예를 들어 철근을 무시한 상태에서 콘크리트의 균열모멘트를 산정할 때 콘크리트의 탄성단면계수(S)를 이용해서 다음과 같이 구합니다.

 

여기서 fr은 콘크리트의 인장응력을 말합니다. 즉 인장응력에 탄성단면계수(S)를 곱하면 균열을 일으키는 모멘트의 크기를 구할 수 있습니다.

 

탄성단면계수와 소성단면계수

우리가 사용하는 대부분의 재료는 힘을 가한 초기 상태에는 탄성상태로 변화하지만 일정한 한도(항복점)를 넘어서면 소성상태를 보입니다. 

 

▶ 응력-변형도 곡선, 탄성과 소성

 

 

따라서 단면계수도 탄성단면계수와 소성단면계수로 나누어집니다. 

 

탄성단면계수(S) : 탄성항복상태일 때의 단면계수

소성단면계수(Z) : 소성항복상태일 때의 단면계수

 

탄성단면계수(S)의 계산

단면계수는 단면에 발생하는 응력이 1일 때 (단위 응력일 때) 단면이 휨모멘트에 저항할 수 있는 크기라고 했는데 이 개념을 이용해서 단면계수를 구해보겠습니다.  다음과 같은 표준단면의 보가 있다고 가정해보겠습니다. 부호를 바꾸어서 사용하겠습니다.

 

 

 

일단 탄성상태일 때는 응력분포가 다음과 같이 나타나는데 응력이 1일 때를 기준으로 하므로 압축측 최외단의 응력과 인장측 최외단의 응력이 1이 됩니다 .

 

이 때 압축응력의 합력과 인장응력의 합력은 다음과 같이 계산할 수 있습니다. 0.5는 평균응력이 됩니다. 

 

이 때, 즉 최외단측 응력의 크기가 1일 때 발생하는 휨응력의 크기는 다음과 같이 계산할 수 있습니다. 

 

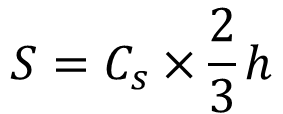
즉 압축응력의 합력 또는 인장응력의 합력에 두 힘 사이의 거리(보 높이의 2/3)를 곱한 값이 됩니다. 이 값을 풀면 다음과 같이 됩니다.

 

소성단면계수(Z)의 계산

소성단면계수는 소성항복상태를 기준으로 하므로 응력분포를 다음과 같이 나타낼 수 있습니다. 

 

응력의 분포가 직사각형은 아니지만 거의 직사각형에 근사하다고 볼 수 있기 때문에 압축측의 합력과 인장측의 합력은 다음과 같이 계산할 수 있습니다. 여기서도 응력은 단위응력 1을 기준으로 합니다.

 

 

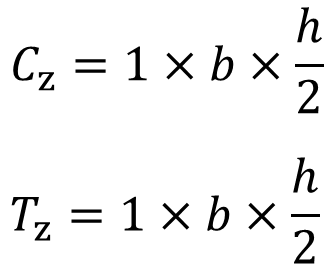
휨응력의 크기는 압축응력의 합력 또는 인장응력의 합력에 두 힘 사이의 거리( 여기서는 거리가 h/2)를 곱한 값이므로 다음과 같이 계산할 수 있습니다.

 

이렇게 보면 탄성단면계수와 소성단면계수가 다르다는 것을 알 수 있습니다.

 

▶ 보 경간과 춤

▶ 보의 처짐과 사용성

 

▶  구조역학 관련 전체 내용 보기

▶ 건축 지식 저장소 전체 내용 보기