상세 컨텐츠
본문
성힌지는 소성설계 개념에서 나온 것으로 지진하중과 관련이 되어 있습니다.
▶ 지진하중(Seismic load, Earthquake load) 개요
▶ 지진하중/ 설계응답스펙트럼이란?/ 설계응답스펙트럼 구하는 방법
지진하중은 매우 큰 하중이지만 발생확률은 매우 낮습니다. 건축물의 내진등급별 최소성능목표를 보더라도 내진등급 Ⅱ인 건축물은 재현주기 1000년인 지진하주에 대해 인명보호를 목표로 하고 있습니다. 이렇게 확률이 높지 않은 지진하중에 대해 탄성범위 내로 설계하는 것은 비효율적이라고 할 수 있습니다. 따라서 탄성을 넘어선 소성구간의 붕괴까지를 감안해서 설계하겠다는 것이 소성설계의 기본 개념입니다.
소성설계의 기본개념
가장 간단한 부정정구조물을 보겠습니다.

이 구조물에 지진하중 p가 작용한다고 할 때, 절점 A가 최대 응력에 도달했다고 가정해 보겠습니다. 이 경우 절점 A는 소성항복상태에 도달하게 되고 더 이상 모멘트를 부담할 수 없는 상태가 되는데, 이 때 A절점은 더 이상 하중을 부담할 수 없으며 무한하게 변형이 증가하는 상태가 됩니다. 즉 A점이 소성힌지가 됩니다.

그러면 구조물이 붕괴될까요? 그렇지는 않습니다. 이 상태가 되었다고 해서 구조물은 불안정상태에 도달한 것은 아닙니다. 3차 부정정에서 2차 부정정상태에 도달한 것일 뿐입니다. 이 구조물은 안정하므로 추가로 힘을 받을 수 있습니다.
여기서 절점의 차원과 구조체 전체의 차원을 구분해서 생각할 필요가 있습니다. 절점의 차원에서는 재료가 항복상태에 도달해서 더 이상 힘을 부담할 수 없지만 구조체 전체는 안정상태이므로 하중을 부담할 수 있습니다.
이 구조물이 최종적으로 불안정한 상태가 되기 위해서는 차수가 0보다 작아야 하므로 4개의 소성힌지가 발생해야 합니다. 즉 3개의 소성힌지가 발생할 때까지는 안정한 구조물을 유지할 수 있습니다. 이것이 소성설계의 기본 개념이다.
소성힌지
점A로 표현된 절점은 Mp만큼 모멘트를 지지하면서 힌지처럼 거동하는 지점이라고도 할 수 있는데, 소성설계에서 소성힌지는 부재의 단면 전체가 소성항복상태에 도달한 상태를 의미합니다.
이렇게 소성힌지처럼 거동하려면 부재는 충분한 연성이 있어만 하고, 강재가 대표적인 연성재료라고 할 수 있습니다.
이론상으로 무한한 변형이 일어나는 지점이라고 할 수 있으며, 응력변형도 곡선에서는 다음과 같이 표현됩니다.

탄성항복상태와 소성항복상태
우리가 사용하는 대부분의 재료는 힘을 가한 초기 상태에는 탄성상태로 변화하지만 일정한 한도(항복점)를 넘어서면 소성상태를 보입니다.
▶ 단면계수의 의미와 계산 - 탄성단면계수/소성단면계수

탄성항복상태는 단면의 일부가 항복응력에 도달하는 상태로서, 단면의 일부가 항복상태에 도달하고 나머지 부분에서 힘을 부담할 수는 있지만 탄성적인 성질을 유지할 수 없는 상태를 말합니다.
탄성항복상태의 모멘트를 My라고 할 때 이 값을 계산해 보겠습니다.
탄성항복모멘트(My)
다음과 같은 보 단면이 있을 때 보에 휨모멘트가 발생하면 상부에는 압축응력이, 하부에는 인장응력이 다음과 같이 나타나게 됩니다. 단면의 중립축에서 가장 먼 위쪽과 아래쪽에는 최대 응력 σy이 나타납니다.
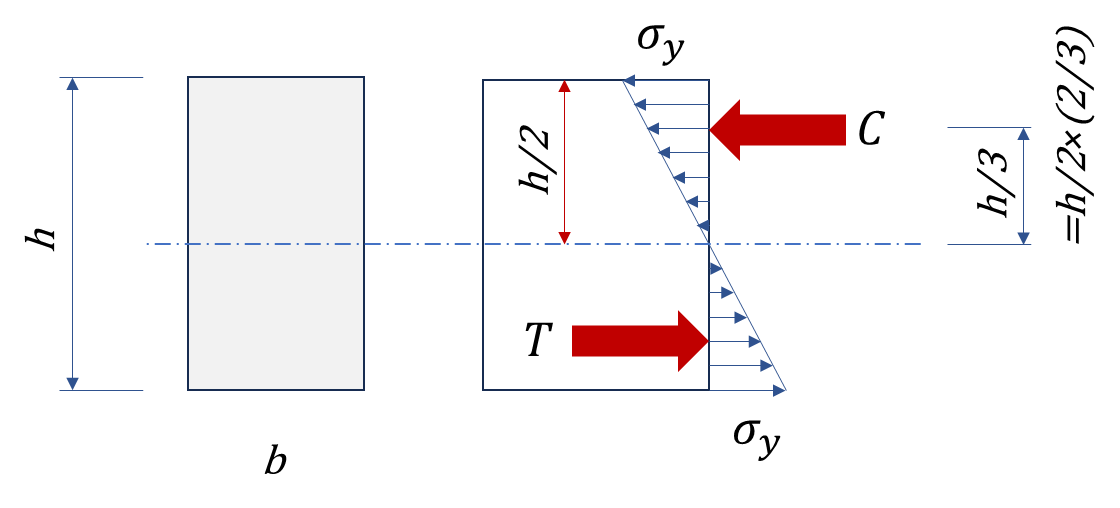
이 때 압축응력의 합력과 인장응력의 합력은 평균응력에 단면의 면적을 곱한 값이므로 다음과 같이 계산할 수 있습니다.

이 때, 휨응력의 크기는 다음과 같이 계산할 수 있습니다.

즉 압축응력의 합력 또는 인장응력의 합력에 두 힘 사이의 거리(보 높이의 2/3)를 곱한 값이 됩니다. 이 값을 풀면 다음과 같이 됩니다.
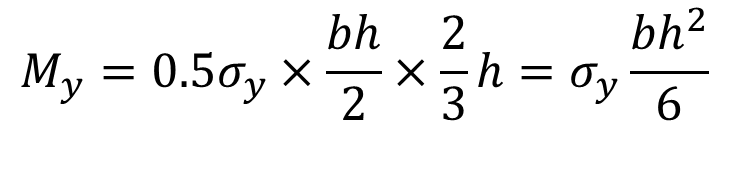
이 식을 보면 최대응력에 탄성단면계수의 곱으로 계산되는 것을 알 수 있습니다. 이 경우에는 전체 단면에서 일부만 항복상태에 도달한 것이고, 나머지 단면의 일부는 힘을 부담할 수 있습니다.
소성항복모멘트(Mp)
비슷한 방법으로 소성항복에 도달할 때의 모멘트(Mp)를 구해보겠습니다. 소성항복상태의 응력분포를 다음과 같이 나타낼 수 있습니다.

응력의 분포가 직사각형은 아니지만 거의 직사각형에 근사하다고 볼 수 있기 때문에 압축측의 합력과 인장측의 합력은 다음과 같이 계산할 수 있습니다.
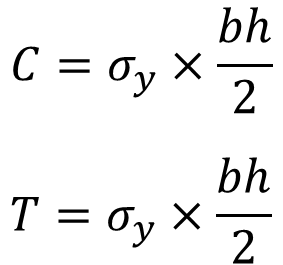
휨응력의 크기는 압축응력의 합력 또는 인장응력의 합력에 두 힘 사이의 거리( 여기서는 거리가 h/2)를 곱한 값이므로 다음과 같이 계산할 수 있습니다.

소성항복모멘트는 최대응력에 소성단면계수의 곱으로 계산되는데, 탄성단면계수와 소성단면계수가 다르다는 것을 알 수 있습니다.
▶ 보 경간과 춤





